![]()
Report the result of the following calculations to the correct number of significant figures.a) 0.347 - 0.0732 Answerb) 23.436 + 82.2 Answer |
Report the result of the following calculation to the correct number of significant figures.c)
|
![]()
![]()

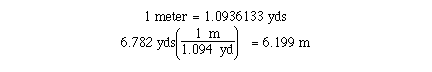
![]()
![]()
Perform the following conversion and report the answer to the correct number of significant figures.a) Determine the number of kilograms in 115 pounds might require 2 unit conversion factors. Answerb) b) Determine the number of gallons in 125 mLs. Answer
|
![]()
Perform the following conversion and report the answer to the correct number of significant figures.b) If a sample of gold measured 17 meters on a side, calculate the mass of the sample. Answerc) The estimated water content in moon rock is 0.1 % by mass. Determine the mass of moon rock needed to extract 1 gallon of water. Answer |
![]()
![]()
Conversions between temperature scales.a) Which temperature is lower? 0 degrees C or 0 degrees F. Answerb) Which temperature is lower? -50 degrees C or -50 degrees F. Answer |