In class on Wednesday we introduced the concept of specific heat and worked several problems using specific heat. In the first of these problems we calculated how much heat was required to change the temperature of a sample of water from 25 C to 60 C. Since this temperature range is within the liquid phase we used the specific heat of liquid water to calculate how much heat was required to change the temperature of the sample of water. But what happens if we needed to know how much heat was required to change the phase of a pure substance, like water?

If we consider a sample of water as a solid, we must add heat to melt the solid. When ice melts, or any solid melts, the liquid is formed. The addition of heat causes a phase change. The heat is absorbed by the particles in the solid causing them to vibrate more rapidly until they have sufficient energy to overcome some of the attractive forces which work to hold the particles in a fixed position. Since the addition of heat is required to change the phase from solid to liquid, the process of melting is endothermic. Heat is absorbed by the solid when changing phase to a liquid. The amount of heat required to change one mole of a substance from the solid phase to the liquid phase is called the molar heat of fusion. For water the value is 6.01 kJ^.mol^-1.

If a sample of liquid water is heated its temperature changes until it reaches 100 degrees C at which point is begins to boil. The change from liquid phase to vapor phase is called vaporization. It is also an endothermic process. The molar heat of vaporization for water is 40.67 kJ^.mol^-1. A considerably greater amount of heat is required to convert a mole of liquid water to vapor.

The reverse process, the conversion of water vapor to liquid is called condensation. This is an exothermic process, that is as water vapor condenses heat must be removed from the water molecules. In the liquid phase as more heat is removed the liquid can be cooled and eventually a solid is formed. The conversion from liquid to solid is called freezing.

So we have discussed four different phase changes. There are still two more. The last two phase changes do occur for water, but they are not as common as they are for another substance called carbon dioxide. When a solid is converted directly into a gas the process is called sublimation. This is also an endothermic process. The enthalpy of sublimation is equal to the sum of the heat of vaporization and fusion. The reverse process, the change from gas to solid is called deposition. It is exothermic.

If we consider a sample of water in the solid phase at -25 degrees C and we add heat it is interesting to plot the change in heat (enthalpy) versus temperature. Some interesting features are apparent in such a plot. Here is an animation of what happens as heat is added to a sample of water at this temperature.

If you can not load the animation here is a narrative of what happens (even if you can view the animations the narrative is handy).

As heat is added to the solid at -25 degrees C it begins to warm. The added heat changes the temperature of the solid. The slope of the line is related to the specific heat of the substance. For ice the specific heat is 2.09 J^.g^-1.C^-1. When the temperature of the sample reaches 0 C, the melting point of water, the added heat is used to break down the attractive forces which maintain the solid phase. The amount of heat required to melt 1 mol of water (solid to liquid) is 6.01 kJ. After the sample has melted the added heat changes the temperature. The change in temperature depends on the amount of substance and the amount of heat added. The specific heat for water in the liquid phase is 4.184 J^.g^-1.C^-1. The temperature continues to increase as heat is added until the boiling point of the liquid is reached. At that temperature the added heat is again required to change the phase of the sample. The temperature remains constant until all of the sample is vaporized. For water the amount of heat required to vaporize a mol of water is 40.67 kJ. It is interesting that it requires so much more heat to vaporize a liquid, compared to melting a solid.

The total amount of heat required to change the temperature of a sample of a compound is just the sum of the heat used in each stage of the process.

Here is a sample problem;

Here is a table of important thermodynamic data for water;

Calorimetry

Our goal in this chapter it to introduce experimental procedures and equipment to determine the heat associated with chemical reactions. For most reactions determining whether the reaction is exothermic or endothermic can be accomplished through observation. Does the reaction container warm or cool. Next is a more quantitative method for determining the amount of heat released or absorbed.

Using calorimeter which is a piece of equipment which uses the change in temperature of a known mass of water to determine the amount of heat transferred in a chemical reaction. Knowing the specific heat of water is an extremely useful piece of physical information. For example, if we performed a chemical reaction in water, the heat given off by the reaction would be absorbed by the water. If we know that the heat absorbed by the water is related to the heat given off by the reaction it would be possible to characterize how much heat can be produced or absorbed in particular reactions.

There are two different types of calorimeters used to determine the heat associated with a chemical reaction. A bomb calorimeter is used to measure combustion reactions and measures the amount heat transferred at constant volume. The other calorimeter, a coffee-cup calorimeter measures the heat transferred in chemical reactions which occur in aqueous solution. A coffee-cup calorimeter measure the heat transfer at constant pressure. Both of these calorimeter are shown in this animation.

The concept of specific heat is extremely useful. For if we perform a chemical reaction in a measured amount of water (we know the mass) and we measure the temperature change the sample of water experiences, it is possible to calculate how much heat was absorbed by the water. We can use the 1st law of thermodynamics to relate the heat given off in a chemical reaction to the heat absorbed by the water (and calorimeter).

When the reaction occurs in the water, assuming it is exothermic, both the water and the calorimeter absorb the heat liberated in the reaction.

heat_system = -(heat_water + heat_calorimeter)

or,

q_system = -(q_water + q_calorimeter)

When using a coffee-cup calorimeter, the reaction occurs in the water usually forming a solution.

q_system = -(q_solution + q_calorimeter)

where qsolution is defined as,

Generally, for a first approximation the specific heat of the solution is assumed to be equal to the specific heat of water. However, the mass of a solute must be added to the mass of water.

To determine the amount of heat absorbed by the calorimeter we use another physical quantity called heat capacity. Heat capacity is a measure of the amount of heat required to change the temperature of a body (whose mass is constant) by 1 degree C. We use the symbol C for heat capacity.

When solutes are added to water the solution process may be exothermic or endothermic. For example, when NaOH_(s) is added to water the reaction which occurs is described by the equation; NaOH_(s)--H₂O--> Na⁺_(aq) + OH^-_(aq)

This reaction is exothermic, that is, when NaOH dissolves heat is released. Here is a problem which allows the determination of how much heat is released per mol of NaOH.

Sample Problem #1 (Calorimetry)

Here is another sample problem using a coffee-cup calorimeter;

Sample Problem #2 (Calorimetry)

We use a device called a bomb calorimeter to measure the change in the internal energy at constant volume. Let's look at a bomb calorimeter. While coffee-cup calorimeters are used to measure the heat released or absorbed in reactions which occur in solution, bomb calorimeters are used to measure the heat released in combustion reactions. Let's look at two problems using a bomb calorimeter;

Sample Problem #3 (Calorimetry)

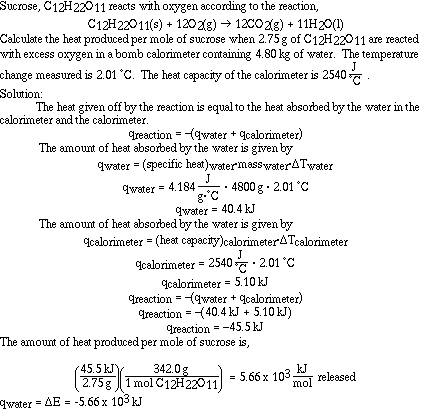
Here is another sample problem using a bomb calorimeter;

Sample Problem #4 (Calorimetry)

Go to Monday, October 13, 1997 Lecture