In this investigation, plastic spheres are used to study the regular geometric shapes of metal and ionic crystals. The regular geometric shapes of crystals reflect the orderly arrangement of the atoms, ions, or molecules that make up the crystal lattice.Three types of packing in crystals will be investigated-hexagonal close packing, face-centered close packing, and body-centered packing-using equivalent spheres. From the models it will be possible to determine the coordination number of the particles of each structure.
The relative sizes of cations and anions that make up ionic crystals are a determining factor for the coordination number. The effect of size as indicated by ionic radius on coordination number will be examined by building models of rock salt (NaCl) and Wurtzite lattices (ZnS).
To gain familiarity with the geometry of metallic and ionic crystal structures.
Wear protective goggles and apron throughout the laboratory activity.
Secure the following per group of two students: 36 two-inch, 13 one-inch, and 13 three-quarter-inch expanded polystyrene spheres. Toothpicks or short lengths of pipestem cleaners can be used as connectors for the spheres.
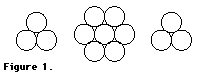Part I
2. Place one three-sphere layer on the table or desk so that one apex of the triangle faces you. Then place the seven-sphere layer on top of the three-sphere layer so that the center sphere fits into the depression at the center of the first layer. Now place the second three-sphere layer over the center sphere so the top layer is directly above the bottom layer. This resulting structure represents hexagonal close packing (hcp).
3. Count the number of spheres closest the central sphere in the structure. This is called the number of nearest neighbors or the coordination number. Zinc, magnesium, and many other metals pack in this manner. Retain this model for Step 3. Answer Implications and Applications question 1 now.
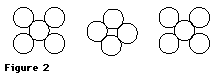
Place one five-sphere layer on the table or desk. Then place the four-sphere layer over the first so that the four spheres rest in the spaces between the corner spheres in the bottom layer. Now place the last five-sphere layer on top so that it is situated directly over the bottom layer. Study the structure carefully and decide why it is called face-centered cubic (fcc). Copper, silver, aluminum, and many other metals pack in this manner in crystals. Determine the coordination number. Answer Implications and Applications question 2 now.
 |
TABLE OF CONTENTS | TOPIC OVERVIEW | CONCEPT/SKILLS DEVELOPMENT | LINKS/CONNECTIONS | EXTENSIONS |  |
|---|