Chapter 12

PROPERTIES OF SOLIDS

The physical properties of crystals are determined by the kinds of particles they are composed of, and the attractive forces that occur between those particles. Some examples of the variety of physical properties which we observed in solids are listed below;

1. Diamond is an extremely hard substance

2. Graphite is a very good lubricant

3. Both dry ice (solid carbon dioxide) and ice are soft

4. Metals are good conductors

All of these properties depend on;

1. The kind of intermolecular forces

2. Strength of the intermolecular forces

We can divide crystals into types, based on the type of intermolecular attractive forces, which exhibit similar properties. (see Table 11.6 on page 402.)

I. Extended Covalent

(Show diamond example)

Extended covalent (covalent network solids) solids consist of atoms which are held together in large networks containing extended covalent bonds. Quartz is an example of a three dimensional network of covalent bonds. (See pages 873 - 879 in BLB.) Quartz consists of SiO2 groups which covalently bond to other SiO2 groups in all three directions. Notice that all the silicon atom are tetrahedral bonded to oxygen atoms. In diamond (see Figure 11.40(a) on page 403), which is one form of elemental carbon, all the carbon atoms are tetrahedrally bonded in a three dimensional network of covalent bonds. Graphite (see Figure 11.40(b) on page 403) consists of sheets of a hexagonal bonded, sp² hybridized, carbon atoms. The fact that these sheets are layered on top of each other allows for slippage of layers relative to each other making graphite an excellent lubricant.

Extended covalent solids of this type are very hard and high melting. Some properties of the solids mentioned above are;

1. High melting, typically above 1000 degrees C. Diamond melts at 3700 degrees C and boils at 4200 degrees C. Graphite sublimes at 3650 degrees C. Quartz melts at 1713 degrees C.

2. Insoluble in most common solvents

3. Poor electrical conductors. (Graphite is an exception.)

II. Molecular

Molecular solids consist of molecules which are held together by London dispersion, dipole-dipole or hydrogen bonding forces. The solid contains ordered arrangements of atoms or molecules which organized, relative to each other, in an orderly three dimensional pattern. Solids of this type are soft and low melting.

III. Metallic

Metallic solids are though to be made up of positive nuclei orderly arranged with the electrons spread out over the positive nuclei (see Figure 9.2C on page 332). The electrons are not thought of as belonging to a particular nuclei, but to the crystal as a whole. The freedom of these electrons to flow accounts for the high electrical and thermal conductivity of metals. The loosely bound character of the electrons, and their ability to vibrate easily, accounts for the characteristic metallic luster of metals.

IV. Ionic

Ionic solids consist of cations and anions distributed throughout the crystal in an orderly three dimensional pattern. Ionic solids are more complicated in their structure, but can be thought of as an orderly pattern of one ion, generally the anion, with cations positioned in 'holes' between the anions. The occupation of these 'holes' depends on the formula of the ionic compound. Ionic solids are characterized as hard yet brittle substances which are high melting. High melting because the electrostatic attractions of the ionic bonds are stronger than the intermolecular forces for molecular solids.

Internal Structure of Solids

The internal arrangement of atoms, molecules or ions can be determined using x-rays. Recall that x-rays are a form of electromagnetic radiation which are of high energy and frequency and short wavelength. When x-rays are incident on a small crystal of a solid the x-rays are diffracted (scattered) to various angles. A piece of photographic film is used to measure the angles and intensity of the scattered x-rays. X-rays have wavelengths between 0.5 and 3 angstroms which is the same range of the separation of atoms in compounds.

When the x-rays are incident on the crystal most travel throught the crystal undisturbed. However some of the x-rays interact with the electrons around the atoms causing the electrons to oscillate. As a result of the oscillation the electrically charged electrons emit a secondary x-ray. These secondary x-rays interfere constructively and destructively to produce the diffraction pattern.

The diffraction pattern produced by the orderly arrangement of the atoms, ions or molecules in the solid state are unique. By combining the scattering angles and the intensity of the scattered x-ray it is possible for a high speed computer to determine what arrangement of atoms are required to produce the observed pattern. The chemist uses his/her knowledge of the atoms in the solid to make an intelligent guess for the computer to initiate a refinement of the structure. Depending on how good a job the initial guess is, the computer will calculate a reliability factor. If the guess is a good one the percent error will be very small and the chemist can be confident that the three dimensional arrangement is reasonable.

When one looks at a crystalline solid one is struck by their beauty. Perfectly flat faces at simple angles are formed. Here are some examples of crystals; apophyllite, calcite, fluorite, galena, halite, pyrite, quartz, selenite. Beautiful cubes, octahedrons, tetrahedrons and other shapes are found in nature. The symmetry observed at the macroscopic level is a good indication of a high degree of symmetry at the atomic level. We use the concept of a crystal lattice to help simplify our study of the structure of matter in the solid state. A crystal lattice consists of a three dimensional array of points which reproduce the same environment as the atoms, ions or molecules in the structure. So while we will continue our discussion of crystal lattices we can replace a particular point withan atom, ion or molecule to obtain a particular three dimensional atomic arrangement.

If one studies three dimensional arrangements one finds there are a very limited number of possible structures which can be repeated uniformily in 3-dimensional space. In fact there are only seven; cubic, hexagonal, rhombohedral,tetragonal trigonal, orthorhombic, monoclinic and triclinic. Each is characterized with specific edge lengths and angles.

We will study the cubic lattice in detail.

The beauty and order of crystal at the macroscopic level it reflected in the ordered arrangement of the atoms, ions or molecules at the atomic level. From the microscopic level a crystal can be thought of as a three-dimensional ordered arrangement of basic units. The ordered arrangement of the structure of a crystal is described in terms of a lattice. A lattice consists of an ordered arrangement of points/spheres which reflect the pattern of the structure. depending on the chemical nature of the substance each lattice is replaced with an atom, ion or molecule for the actual structure. So a crystal lattice represents the arrangement of lattice points in a crystal.

Before we begin we must mention the concept of a unit cell in a crystal lattice. The unit cell is a very simple three dimensional structure which when repeated in three dimensions will reproduce the original three dimensional arrangement.

Recall that solids are incompressible. This suggests that the atoms in solids are arranged such that there is very little space between themselves.

So the most likely structure for metals is one which uses space efficiently. Lets consider each of the basic structures to show you how they are built and several interesting features of the arrangement of the atoms.

We'll begin with simple cubic. In this arrangement we begin will a layer of atoms such that each of the atoms in a given layer is touching four other identical atoms. Crystals are built when layers of atoms are placed on top of each other. For the simple cubic structure the second layer is placed directly on top of the atoms of the first layer. As you can see each atom touches four atoms in the plane and one atom above and below the plane. Each sphere has a coordination number of six. Each atom is surrounded by six other nearest neighbor atoms.

The simple cubic unit cell contains one atom, molecule or ion. This can be understood if we imagine the one-eighth portions of each corner translating to the center and arranging themselves into a single sphere.

This arrangement of atoms is no a particularily efficient way of packing. Only 52 % of the available space is actually occupied by spheres in the simple cubic structure. This means 48% of the unit cell is empty. A portion of the empty part of the simple cubic unit cell is defined as a simple cubic hole. When we discuss ionic compounds we will discuss the occupancy of the hole in the simple cubic structure. Of the 108 elements in the periodic table only polonium packs as a simple cubic structure.

Next we looked at the body-centered cubic lattice (see Figure 12.28 in Silberberg). We saw the body-centered cubic unit cell and how they can be used to build the original structure. The body-centered cubic lattice contains two atoms, molecules or ions in the unit cell. One from the eight, one-eighth portions of each corner atom and one form the body-centered atom.

This structure uses 68 % of the available space. So it is more efficient than simple cubic. Metals which crystallize in a body-centered cubic structure include Group IA metals and the heavier members of Group IIA and several of the early transition metals elements, Ti, V, Cr, Mo, W and Fe.

Next we discussed the relationship between edge length and radius of a metal atom in the simple and body-centered cubic lattices. In the simple cubic lattice the corner atoms are touching each other so the edge length of the unit cell is equal to two metallic radii.

Simple Cubic: e(edge length) = 2r

For body-centered cubic the only place metallic atoms are touching is along a body diagonal. The body diagonal is a straight line which runs from one corner atom through the body-centered atom to the opposite corner atom. We can obtain a relationship between the edge length (e) of the body-centered cubic lattice and the radius (r) using the following approach;

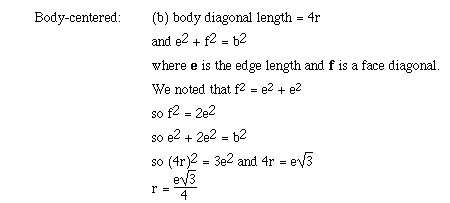
The remaining two structures, the closest-packed structures are the most efficient in packing the atoms into the layers. In the closest-packed arrangement each atom in a layer is surrounded by six other atoms. Each of the additional layers have the identical arrangement of the atoms. Each subsequent layer of atoms is stacked such that the atoms in the layer are packed into the triangular holes in the previous layer.

After building up the second layer we must consider how the third layer of atoms is to be placed. Because it is in the placement of this third layer of atoms that we obtain the two different closest-packed arrangments of atoms. The third layer can either be placed into the triangular holes which result in identical position as the atoms in the first layer or into trianglar holes that produce a layer different in position compared to the first two layers.

If the atoms are placed into the triangular holes which correspond to identical positions as the first layer, the structure is referred to as hexagonal closest-packed. The ABABAB... alternating arrangement of the layer uses the space efficiently (74 %). An atom in a particlar layer is surround by six atoms in the same layer and three atoms in the layers immediately above and below. The coordination number of any atom is 12 in both closest-packed structures.

Metals such as Be, Co, Mg and Zn crystallize in the hexagonal closest-packed structure.

The last structure, cubic closest-packing results when the third layer is placed above the holes which were not used by the atoms of the second layer. This produces an ABCABC... arrangement. The fourth layer is than identical to the first. Again the coordination number is 12 for each of the atoms.

We have discussed two types of cubic structures thus far; simple cubic and body-centered cubic. The cubic closest-packed structure gives rise to a third cubic arrangement of atoms, called face-centered cubic. We looked at another animation to see how it is possible to build up a cubic closet-packed structure and obtain a face-centered cubic lattice. The face-centered cubic lattice contains four atoms, molecules or ions. One from the eight, one-eighth portions of each corner atom and three from the six one-half portions of the face-centered atoms.

The relationship between the edge length of the face-centered cubic lattice and the radius of the metal atom can be obtained as follows;

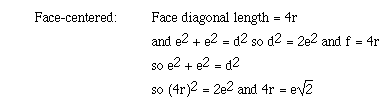
Next we introduced the concept of tetrahedral holes and octahedral holes found in the face-centered cubic lattice. These two holes are important when discussing ionic crystal lattices. Many ionic crystal form from a regular arrangement of the anions with the cations occuping octahedral or tetrahedral holes.

Diamond and silicon are examples of extended covalent solids inwhich the carbon, or silicon, atoms form a face-centered cubic lattice and half of the tetrahedral holes are occupied with carbon or silicon atoms.

The octahedral holes in the closest-packed structure are found between two adjacent sets of three atoms. The coordination number for an octahedral hole is six. In the face-centered cubic lattice the octahedral holes are located on the edge-centered positions and in the middle of the face-centered cube. This gives rise to a total of four octahedral holes in a face-centered cubic structure.

We next reviewed a number of ionic compounds (to view the graphics you will need the ChemScape Chime (see Plug-ins Link). Our approach involved identifying a basic lattice of anions (most typical) or cations and then identifying the location of the opposite ion within holes in the basic structure. For example in the sodium chloride structure the chloride ions formed a face-centered cubic structure with sodium ions in every octahedral hole. This gives rise to a total of four NaCl units in the sodium chloride unit cell. The four chlorides are derived from the eight corner ions and the six face-centered ions. The four sodium ions are derived from the occupancy of the octahedral holes.

The cesium chloride structure consisted of a simple cubic arrangement of chloride ions with cesium ions found at the center of the simple cube (in the simple cubic hole).

In the zinc sulfide (zinc blende) structure the zinc cations formed a face-centered cubic lattice with the sulfides occupying half of the tetrahedral holes.

Calcium floride, CaF2, structure consists of a basic face-centered cube of calcium ions. Where do you think the fluoride ions are located?

Several other interesting structures were viewed including a perovskite structure.

Next we looked at a problem involving a gold lattice structure. Gold crystallizes in a face-centered cubic lattice with its edge length equal to 4.079 Angstroms;. From this information determine the density of gold and its atomic radius.