We began Chapter 12 reviewing our particulate level view of the three phases of matter; gas, liquid and solid. We noted in a solid the atoms or molecules are tightly packed with little free space for the particules to move around. In a liquid the particles are still tighly packed, but there is more space available for particles to move. Liquids can flow, so the atoms or molecules can move relative to each other. In a fas the particles are well separated from each other in space. Gases also flow, and can be compressed easily. These representations are important for us to have as images to understand the content of this chapter.

In terms of energy how do we view the three phases of matter and there transitions between phases. We view a diagram depicting the three phases of matter on an energy scale and we discussed it in detail. Beginning with the solid phase it has the lowest energy. To move to the liquid phase we must add energy. The transition from solid to liquid, melting, is endothermic (we must add energy). When a liquid freezes the process is exothermic. Heat flows from the liquid water to the surroundings. We place liquid water in a freezer, a region where the temperature is below the freezing point of water, and heat flows from the liquid water into the surrounds causing the water to freeze. The liquid phase is higher in energy compared to the solid phase. The gas phase is even higher in energy. The phase change from liquid to vapor (gas) is called vaporization and it is endo thermic. When the vapor phase condenses to the liquid the process is exothermic. Anyone who has burned themselves by coming in contact with steam understands the amount of heat associated with the condensation of water vapor. The phase change from solid to vapor is called sublimation, while from vapor to solid it is called deposition. In this discussion our goal is to become familiar with the terms used to describe the different phase transitions and to understand in qualitative terms the energy flow that occurs in the transitions.

Next we viewed an animation showing a particulate level view of the three phases as the temperature of a sample is cooled. A container of gas particles was cooled. As the temperature of a collection of particles was lower we observed the particles slowing down. At the lower velocities colliding particles appeared to stick together forming groups of particles. As the temperature continued to drop the number of particles in these groups increased. Eventually the groups of particles are of sufficient size that they fall to the bottom of the container as a result of force of gravity, forming a liquid. As the temperature continues to drop the particles become more ordered, and their translational energy drops to a very small value and a solid forms. Condensation occurs when the intermolecular attraction between a pair of particles exceeds the kinetic energy of the collision.

The 'stickyness' exhibited by particles at the lower temperatures, which result in the formation of liquids and eventually solids is due to intermolecular attractive forces. Intermolecular means between molecules. Intramolecular means between atoms. Intramolecular forces are what we call covalent bonds and are very strong (100 - 1000 kJ/mol). Intermolecular forces are between molecules and are weak (0.1 - 40 kJ/mol). Intermolecular forces are less directional compared to covalent bonds and operate over a longer range compared to covalent bonds. It is intermolecular forces which explain the formation of liquids and solids in covalent compounds. Intermolecular attractive forces are electrostatic in nature.

Intermolecular forces are classified into the following categories;

* ion-dipole

* dipole-dipole

* induced dipole-induced dipole (London dispersion forces)

* hydrogen-bonding

We will discuss these different intermolecular attractive forces in a few lectures.

Next we explored the in more detail the energy changes associated with phase transitions. We viewed a diagram called a heating curve showing enthalpy (heat) on the y-axis and temperature on the x-axis. In the heating curve we observe that as heat is added to a sample, beginning with a solid, the temperature of the sample begins to increase linearly. The temperature of the sample continues to increase until we reach the melting point of the solid. At the melting point the temperature of the sample does not change as heat is added. The reason for this is the heat being added is used to cause a phase change from solid to liquid. As mentioned earlier the intermolecular attractive forces between the atoms of molecules in the solid phase must be overcome (broken) to form the liquid phase. As these intermolecular attractive forces are partially overcome the temperature remains constant. Once all of the solid is melted, the temperature of the liquid increases linearly until the boiling point of the liquid is reached. At this phase change we observe the same behavior as noted in the solid/liquid phase change. The temperature remains constant until all of the liquid is vaporized to a liquid. Again the reason the temperature does not change during the phase transition is the heat is used to overcome the intermolecular attractive forces remaining in the liquid phase. Note the amount of heat required to convert the liquid to its vapor is significantly greater compared to the heat required to convert the solid to its liquid. The amount of intermolecular attractive forces that must be overcome in the liquid to vapor transition is much greeater compared to the solid to liquid transition. Once all of the sample in in the vapor phase the addition of heat causes the temperature of the gas to change linearly again.

Next we discussed in quantitative terms the energy relationships of the different steps as we moved from a solid below its melting point to a vapor above its boiling point. When we begin with a solid below its melting point the change in temperature is controlled by the amount of substance and its specific heat. Recall the specific heat of a substance is the amount of heat required to change the temperature of 1 gram of the substance by 1 degree celsius. For solid water the specific heat is 2.09 J g^-1 C^-1. So if we know the mass of the solid water and the temperture change we can determine how much heat is absorbed. At the melting point the amount of heat absorbed during the phase change is determined by the enthalpy of fusion, delta H_fusion. For water the enthaply of fusion is 6.01 kJ mol^-1. Notice there is no temperature term in the heat of fusion. Recall the temperature remained constant during the phase transition from solid to liquid. In the liquid phase the heat required to change the temperature of 1 gram of water by 1 degree Celsius is 4.184 J g^-1 C^-1. The heat of vaporization for water is 40.67 kJ mol^-1. The specific heat for the solid phase of water is 1.84 J g^-1 C^-1. So how do we combine all this information to determine the heat required to change the temperature of a sample of water?

Here is a summary table of the specific heats and enthalpy of phase changes for water;

Let's look at several sample problems;

How much heat is required to change 36.0 g of H₂O(l) at 100 deg C to 36.0 g of H₂O(g) at 100 deg C? Answer

How much heat is required to convert 30.0 g of H₂O(s) at -10 deg C to 30.0 g of H₂O(g) at 110 degC. Answer

The specific heat of iron is 0.433 J g^-1 C^-1. What is the final temperature if 45.0 g of iron, initially at 95 deg C, is added to 100.0 g of water at 23.0 deg C? Answer.

Evaporation

Imagine a sample of a liquid in a beaker left out in a warm room for an extended period of time. What happens to the liquid in the beaker? It evaporates, that is, if we left the beaker there and returned after several days we would expect all the liquid to be gone. Where did it go? Into the atmosphere. How does the liquid, like water, at room temperature, evaporate?

How do we understand the nature of evaporation? Can we use the kinetic molecular model to explain evaporation? And if we can, what new properties might the model lead us to consider?

In a sample of a liquid the particles are in constant, chaotic motion (here is the animation we used in class). At the particular temperature the particles of a liquid have an average kinetic energy. But remember there is a distribution of energies do that some particles have a high energy and some have low energy. If a particle in the liquid phase has enough energy and its velocity vector is oriented in the proper direction it can escape into the vapor phase. Even though vaporization is an endothermic process since the liquid is in a large room at constant temperature the room maintains the temperature of the liquid. If the beaker is left open to the atmosphere eventually all of the liquid evaporates. If we place a lid over the beaker to prevent the escape of the water vapor in the room the volume of the water will not change. In this case the water molecules escape into the air above the surface of the liquid. After a while, when the number of molecules of water in the air above the liquid become large, some molecules in the vapor phase condense by colliding with the liquid. After a period of time the rate of escape of molecules from the liquid phase equals the rate of condensation of vapor into the liquid phase. When this occurs the system is in equilibrium. That is the two rates are equal, and there is no net change. If a particle in the vapor phase condenses, an instant later a particle evaporates. The system is in a state of dynamic equilibrium. That is particles are constantly changing from vapor to liquid phase and visa versa. However, if we measure the vapor pressure of the sample we see there is no change in pressure over time. The pressure exerted by the water molecules in the vapor phase, above the liquid, is called the vapor pressure of the liquid at the particular temperature.

Next we continued our discussion of vapor pressure of liquids by turning our attention to a demonstration setup showing three barometers. (Here is an animation of the demonstration we performed live in class.) The glass tubes contained mercury. No (ideally) air molecules are found in the space above the mercury, i.e. a vacuum.

A sample of liquid introduced at the bottom of the column the liquid will rise up the tube to the top of the mercury, because of density differences. When the reaches the space above the mercury the liquid will immediately vaporize to an extent equal to or less than the vapor pressure of the liquid at the particular temperature. Whether the pressure exerted is equal to the vapor pressure of the liquid depends on the amount of liquid injected. If we introduce water, ethanol and ether into different columns we can see the difference in the vapor pressure, at room temperature of each liquid. Water first. Notice the difference in the height of the column of mercury after introducing the water sample. The change in height is equal to the vapor pressure of the water (23.7 mmHg) at 23 degrees C. Notice there is a small amount of liquid water resting on the surface of the mercury. Next we'll try ethanol. Notice the vapor pressure of ethanol is greater at the same temperature (55 mmHg). Finally we tried ether. First a small amount. We noticed the height of the column of mercury, but also notice that there was no liquid on the surface of the mercury. This meant that all of the liquid introduced vaporized. It all vaporized because the resulting pressure exerted by the sample of ether is smaller than the vapor pressure of ether. So more ether had to be added. And the level of the mercury drops even further. Finally it has reached a level equal to the vapor pressure (diethyl ether it is 520 mmHg).

Next we looked a plot of vapor pressure (y-axis) versus temperature (x-axis) and observed the exponential increase in vapor pressure with temperature. We also discussed the definition of a boiling point. The correct definition of boiling point is the temperature at which the vapor pressure of a liquid equals atmospheric pressure. With this definition we can understand why liquids boil at lower temperatures when heated at high altitudes. At high altitudes the atmospheric pressure is lower, there is less atmosphere above the surface at high altitudes. If the atmospheric pressure is lower water will boil at a temperature at which the vapor pressure is equal to the atmospheric pressure. This is a lower temperature. I can get water boiling at room temperature. How hot is water boiling at room temperature?

The normal boiling point of a liquid is the temperature at which the vapor pressure equals 1 atmosphere.

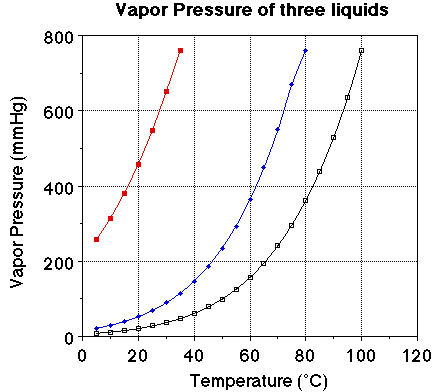
We we looked at the plot of vapor pressure versus temperature we noted the plot of the three liquids were very similar. The obvious difference is the boiling point for the three liquids. The vapor pressure of each of the liquids at 25 degrees C should be noted. The vapor pressure of water at 25 degrees C is 23.7 mmHg, for ethanol it is about 55 mmHg and for diethyl ether it is 520 mmHg. Notice the boiling points for the three liquids. Water boils at 100 degrees C, ethanol at 78. 3 degrees C and ether at 34.6degrees C. At a given temperature a comparison of the vapor pressure suggests the liquid with the highest vapor pressure will have the lower boiling point. At a given temperature a high vapor pressure indicates there is a large number of molecules of the substance in the vapor phase. The more molecules in the vapor phase at a given temperature the easier it is for the molecules to escape into the vapor phase. The greater the number of molecules in the vapor phase at a given temperature the weaker the attractive forces between the molecules and the lower the energy required to vaporize the molecules. That is there is a relationship between the heat of vaporization and the vapor pressure of a liquid.

Looking at the plot of vapor pressure versus temperature we can see the exponential curve. However, if it were possible to obtain a straight line from the data it would be more useful. If we instead plot the natural log (ln) of the vapor pressure versus 1/T (K) we do obtain a nice linear relationship.

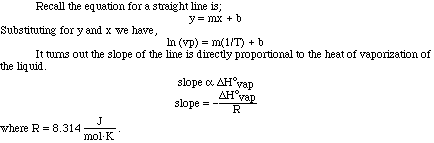
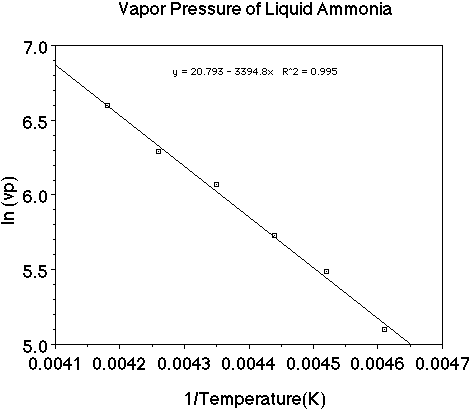
Let's use a set of data as an example and plot the data to see how the heat of vaporization of a liquid can be determined. (Here is an animation of this problem.)

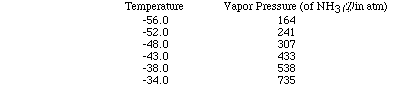
Want to try a few problems?

Problem #1...graphing

Problem 2

Problem 3