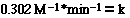Untitled Document

Lecture Notes for Chemical Kinetics

Chemical kinetics concerns itself with what happens while a reaction is underway, not just in the final outcome. Chemical kinetics does not change the chemical reaction it simply provides a clearer picture of what happens during the progress of the chemical reaction. With the new knowledge it will be possible to control the conditions of a reaction which will help increase the amount of the desired products. If we were able to travel to the molecular level and watch the progress of the reactants in the course of the reaction and the many changes they undergo in proceeding to the products we would be doing chemical kinetics. If we were able to observe first hand how the electrons behaved during a chemical reaction we would be doing chemical kinetics.

But, unfortunately, we can not 'see' molecules or electrons with our own eyes so it is impossible to view these molecular and electronic interactions firsthand. What we do instead is to use instruments that follow the reaction, by watching properties of particular reactants that depend upon their concentration. This way we can watch how a reactant disappears in a chemical reaction. Or we can watch the properties of a particular product that depend upon concentration and we can see how its concentration changes during the course of a chemical reaction. Then by applying mathematical models and doing some calculations it is possible to understand the pathway a reaction follows. The best way to try to understand reactions in this way is to study how fast the reactions occur-to study the rate of a chemical reaction.

We will find that reactions, even reactions that are unrelated chemically, exhibit behavior associated with the speed that allow a chemist to classify them in a limited number of catagories.

So in summary chemical kinetics is the study of;

1. the rate at which reactants are converted to products during the course of a chemical reaction.

2. The factors, which include temperature, pressure, concentration, catalyst and surface area that effect the rat of a chemical reaction.

3. The sequence of steps, or the mechanism, which we believe occurs when reactants are converted to products.

Rates of chemical reactions depend upon; Concentration, Temperature and Catalyst. Our first step is to understand the term reaction rate.

To begin we must discuss the term rate. Rate is a measure of how fast or slow a process will occur and is usually describe as a ratio of an event with time. The speed that we drive an automobile is expressed in miles per hour. Filling a sink or bathtub with water from a faucet. The faucet delivers water at a rate of gallons per minute. Rate in each case is similar in that it is a change in a quantity with time.

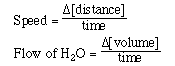
For a chemical reaction its rate, rate of reaction, is expressed in terms of how fast the concentration of a substance changes in the course of a chemical reaction.

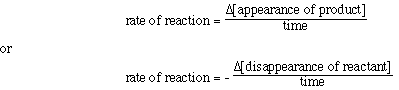
For the reaction

2N₂O₅(g) ---> 4NO₂(g) + O₂(g)

the rate can be expressed in terms of the reactant or any of the products.

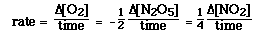
We can understand the different forms of expressing rate by thinking about what is happening in the reaction. According to the balanced chemical equation everytime 1 mol of O₂ is formed 4 mol of NO₂ react. Therefore, NO₂ is formed 4 times as fast as O₂ is formed. To equate the rate of formation of O₂ to the rate of formation of NO₂ we need to include a multiplier to get the two rates equal. We see this above.

Try a sample problem.

In the upper atmosphere the following reaction occurs to produce ozone, O₃;

3O₂(g) ---> 2O₃(g)

If the rate of disappearance of O₂ is 2.17 x 10^-5 mol L^-1 S^-1 what is the rate of appearance of O₃?

Answer

How do we determine a rate of reaction for a reaction? Well, this is accomplished by measuring the change in concentration of a reactant or product with time, and then graphing the experimental data. The rate of change of concentration with time can then be determined from the graph of the data. Lets consider some experimental data for a reaction and discuss how we measure the rate of a reaction. The reaction of interest is;

2NO₂(g) ---> 2NO(g) + O₂(g)

The data is;

[NO₂]	0.350 M	0.245 M	0.190 M	0.130 M	0.090 M	0.062 M
time (min)	0	4	8	16	24	40

Our approach to interpreting rate information from this data is to plot the data. [NO₂] is on the y-axis and time is on the x-axis. The graph appears as the following;

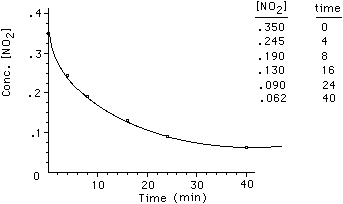
To determine the rate of the reaction we must find how [NO₂] changes with time. For this reaction we have that;

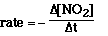
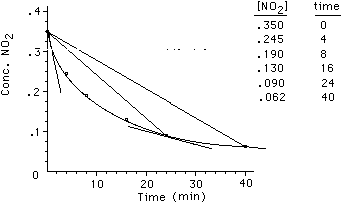
Concentration is in mol/liter, M, so rate has units of M/time. We can use any time unit in the denominator. For this experiment we are using minutes. The negative sign indicates that the [NO₂] is decreasing with time.

To begin we must recognize that there are several different types of rates that can be determined from this plot. We can calculate the rate of the reaction by calculating the change in [NO₂] with a change in time from two data points on our plot. For example, we can determine the rate of the reaction by selecting the first data point and the last date point. Drawing a line between the two selected data points, we can determine the slope of the line which is the rate between these two data points.

rate = -(0.35 - 0.062)/(0 - 40) = 7.2 x 10^-5 M min^-1

This rate is called an average rate. Anytime a line is drawn between two points on the data curve we are calculating an average rate.

Calculate the average rate between 0 and 24 minutes. Answer:

Notice that the ratio of concentration to time is larger, that is, the average rate is faster between 0 and 24 minutes compared to the average rate between 0 and 40 minutes. The rate between 0 and 8 minutes is 2.0 x 10^-2 M min^-1, faster yet. Another type of rate that can be determined on such a plot is an instantaneous rate. Such a rate is determined by drawing a line tangent to a point on the curve.

Another type of rate is called the instantaneous rate. The instantaneous rate is the rate at a particular time. It is not an average rate over a time interval. For example, the instantaneous rate at 24 minutes 3.2 x 10^-3 M min^-1. This value is obtained by drawing a line tangent to the curve at 24 minutes. The slope of thetangent line is the instantaneous rate. The instantaneous rate at 8 minutes is 1.0 x 10^-2 M min^-1, and at 0 minutes the instantaneous rate is 3.7 x 10^-2 M min^-1. The rate at t = 0 is the fastest rate the reaction can have and is called the initial rate. The rate decreases from this point on as reactants are consumed. It is the initial rate that we are most interested in measuring for a chemical reaction. We can see from this single experiment that the rate of the reaction depends on the concentration of the reactants. That is, we have shown that as the concentration of NO2 decreases so does the rate. Here is an animation of the data and how to obtain an average, instantaneous and initial rate.

What happens if we try a second experiment in which we begin with a new initial concentration of NO₂. The data that I have is as follows;

[NO₂]	0.700 M	0.379 M	0.258 M	0.158 M	0.115 M	0.074 M
time (min)	0	4	8	16	24	40

The plot of this data looks like;

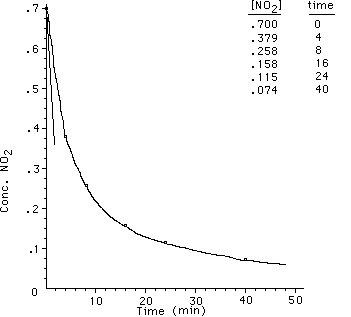
The initial rate for the second set of data is 1.5 x 10^-3 M min^-1.

So from the two experiments lets summarize the important information. We did the same reaction for each experiment, at the same temeprature and other conditions. The only thing different between the two experiments was the initial concentration of [NO₂].

Experiment	[NO₂]	Initial Rate (M min^-1)
1	0.350 M	3.7 x 10^-2 M min^-1
2	0.700 M	1.5 x 10^-1 M min^-1

The data clearly says the initial rate of the reaction is dependent on the initial concentration of NO₂. From this knowledge of the dependence of the initial rate of a reaction on the initial concentration of NO₂ it is possible to determine the rate equation for the reaction. The rate equation gives the mathematical relationship between the reaction rate and the concentration of one or more reactants. Here is an animation of the data and how to obtain an average, instantaneous and initial rate.

From the data we see going from Exp 1 to Exp 2 we doubled the [NO₂].

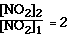
Whan happened to the ratio of the initial rates?

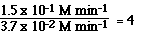
Had we tripled the initial concentration of NO₂ the initial rate would have increased by a factor of nine.

So how do we interpret this information...;

[NO₂] increase by factor of 2 the rate increases by a factor of 4

[NO₂] increase by factor of 3 the rate increases by a factor of 9

So the rate increases by the square of the concentration. We could write a relationship mathematically that reflects the experimental data;

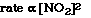
The exponent used with the [NO₂] is called the order for NO₂. We say the order of the reaction with respect to NO₂ is 2. Or we say the reaction is second order in NO₂.

To convert the relationship from a proportionality to an equality we need to add a constant. We will use 'k' to represent the constant and we will call the constant the rate constant. The new equation now becomes;

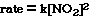
This is called the rate law equation for the reaction. It reflects the relationship betwen the initial rate, the rate constant and the order for each reactant.

For this reaction, under these experimental condition we need to know what the magnitude and the units of k, the rate constant. To determine the rate constant for the reaction we substitute for the [NO₂] and the initial rate from either of the experiments.

So;

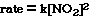
Substituting for Experiment 1

and

Lecture Notes for Chemical Kinetics

We will find that reactions, even reactions that are unrelated chemically, exhibit behavior associated with the speed that allow a chemist to classify them in a limited number of catagories.

So in summary chemical kinetics is the study of;

1. the rate at which reactants are converted to products during the course of a chemical reaction.

2. The factors, which include temperature, pressure, concentration, catalyst and surface area that effect the rat of a chemical reaction.

3. The sequence of steps, or the mechanism, which we believe occurs when reactants are converted to products.

Rates of chemical reactions depend upon; Concentration, Temperature and Catalyst. Our first step is to understand the term reaction rate.

For a chemical reaction its rate, rate of reaction, is expressed in terms of how fast the concentration of a substance changes in the course of a chemical reaction.

For the reaction

2N2O5(g) ---> 4NO2(g) + O2(g)

the rate can be expressed in terms of the reactant or any of the products.

Try a sample problem.

In the upper atmosphere the following reaction occurs to produce ozone, O3;

3O2(g) ---> 2O3(g)

If the rate of disappearance of O2 is 2.17 x 10-5 mol L-1 S-1 what is the rate of appearance of O3?

Answer

2NO2(g) ---> 2NO(g) + O2(g)

The data is;

[NO2]

0.350 M

0.245 M

0.190 M

0.130 M

0.090 M

0.062 M

time (min)

0

4

8

16

24

40

Our approach to interpreting rate information from this data is to plot the data. [NO2] is on the y-axis and time is on the x-axis. The graph appears as the following;

To determine the rate of the reaction we must find how [NO2] changes with time. For this reaction we have that;

Concentration is in mol/liter, M, so rate has units of M/time. We can use any time unit in the denominator. For this experiment we are using minutes. The negative sign indicates that the [NO2] is decreasing with time.

rate = -(0.35 - 0.062)/(0 - 40) = 7.2 x 10-5 M min-1

This rate is called an average rate. Anytime a line is drawn between two points on the data curve we are calculating an average rate.

Calculate the average rate between 0 and 24 minutes. Answer:

What happens if we try a second experiment in which we begin with a new initial concentration of NO2. The data that I have is as follows;

[NO2]

0.700 M

0.379 M

0.258 M

0.158 M

0.115 M

0.074 M

time (min)

0

4

8

16

24

40

The plot of this data looks like;

The initial rate for the second set of data is 1.5 x 10-3 M min-1.

So from the two experiments lets summarize the important information. We did the same reaction for each experiment, at the same temeprature and other conditions. The only thing different between the two experiments was the initial concentration of [NO2].

Experiment

[NO2]

Initial Rate (M min-1)

1

0.350 M

3.7 x 10-2 M min-1

2

0.700 M

1.5 x 10-1 M min-1

From the data we see going from Exp 1 to Exp 2 we doubled the [NO2].

Whan happened to the ratio of the initial rates?

Had we tripled the initial concentration of NO2 the initial rate would have increased by a factor of nine.

So how do we interpret this information...;

[NO2] increase by factor of 2 the rate increases by a factor of 4

[NO2] increase by factor of 3 the rate increases by a factor of 9

So the rate increases by the square of the concentration. We could write a relationship mathematically that reflects the experimental data;

The exponent used with the [NO2] is called the order for NO2. We say the order of the reaction with respect to NO2 is 2. Or we say the reaction is second order in NO2.

To convert the relationship from a proportionality to an equality we need to add a constant. We will use 'k' to represent the constant and we will call the constant the rate constant. The new equation now becomes;

This is called the rate law equation for the reaction. It reflects the relationship betwen the initial rate, the rate constant and the order for each reactant.

For this reaction, under these experimental condition we need to know what the magnitude and the units of k, the rate constant. To determine the rate constant for the reaction we substitute for the [NO2] and the initial rate from either of the experiments.

So;

Substituting for Experiment 1

and

2N₂O₅(g) ---> 4NO₂(g) + O₂(g)

In the upper atmosphere the following reaction occurs to produce ozone, O₃;

3O₂(g) ---> 2O₃(g)

If the rate of disappearance of O₂ is 2.17 x 10^-5 mol L^-1 S^-1 what is the rate of appearance of O₃?

2NO₂(g) ---> 2NO(g) + O₂(g)

[NO₂]

Our approach to interpreting rate information from this data is to plot the data. [NO₂] is on the y-axis and time is on the x-axis. The graph appears as the following;

To determine the rate of the reaction we must find how [NO₂] changes with time. For this reaction we have that;

Concentration is in mol/liter, M, so rate has units of M/time. We can use any time unit in the denominator. For this experiment we are using minutes. The negative sign indicates that the [NO₂] is decreasing with time.

rate = -(0.35 - 0.062)/(0 - 40) = 7.2 x 10^-5 M min^-1

What happens if we try a second experiment in which we begin with a new initial concentration of NO₂. The data that I have is as follows;

[NO₂]

The initial rate for the second set of data is 1.5 x 10^-3 M min^-1.

So from the two experiments lets summarize the important information. We did the same reaction for each experiment, at the same temeprature and other conditions. The only thing different between the two experiments was the initial concentration of [NO₂].

[NO₂]

Initial Rate (M min^-1)

3.7 x 10^-2 M min^-1

1.5 x 10^-1 M min^-1

From the data we see going from Exp 1 to Exp 2 we doubled the [NO₂].

Had we tripled the initial concentration of NO₂ the initial rate would have increased by a factor of nine.

[NO₂] increase by factor of 2 the rate increases by a factor of 4

[NO₂] increase by factor of 3 the rate increases by a factor of 9

The exponent used with the [NO₂] is called the order for NO₂. We say the order of the reaction with respect to NO₂ is 2. Or we say the reaction is second order in NO₂.

For this reaction, under these experimental condition we need to know what the magnitude and the units of k, the rate constant. To determine the rate constant for the reaction we substitute for the [NO₂] and the initial rate from either of the experiments.