Well what can we do with all this you ask: with this simple
equation
PV = nRT
Essentially, use of this equation boils down to 2 types of
problems.
Single Value
Change of Condition
I. Single Value
In this type of problem three of the four variables are given
and you must solve for the fourth.
P, V, and t solve for n
P, V, and n solve for T
P, n, and T solve for V
n, T, and V solve for P
Here are three sample problems of this type. The first is
trival, the second more interesting and the third even more
interesting.
II. Change of Condition
The characteristic feature of the change of condition
problem, which involves 2 or 3 of the variable n,P, V and T, is
the identification two values for one of P, V or T variables.
Here are three sample problems of this type. .
The approach is to establish which variables in the equation
are constant and which are changing. Separate the variable from
the constants, note the constants are equal, therefore so are the
variables and then solve for the unknown.
Following this approach we can obtain relationships such as;
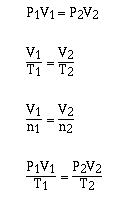
and many more.
Our knowledge of gas laws can be extended to
stoichiometry problems involving gases.
Partial Pressure
If we begin with the ideal gas law,
PV = nRT
we can rearrange the equation to show a relationship between
pressure and the number of moles of gas,
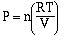
So pressure is directly related to the number of moles of
gas. But suppose the gas is actually a mixture rather than a pure
substance? For ideal gases the total pressure of a mixture is
simply the sum of the pressures of the component gases if they
were alone in the container.
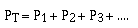
The pressures of the individual component gases, P1,
P2, and P3 are called the partial pressures
of the component gases. So
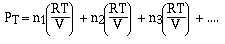
and if we factor out the 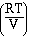 we have,
we have,
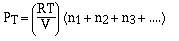
Dalton, who is credited with the above relationship for
partial pressures, was a meteorologist and performed many
experiments working on determining the amount of water vapor
absorbed by dry air at different temperatures. So we can look at
a problem dealing with water vapor.
When a gas is generated the easiest way to collect the gas is
by displacing water from a container. The gas is produced in a
reaction vessel which is vented via a tube to a container of
water. As the reaction proceeds the gas produced displaces the
water in the container. In this way the volume of gas produced in
the reaction can be measured. However, one problem associated
with this experiment involves Dalton's law of partial pressures.
The problem is the gas collected is not pure. It also contains
water vapor. It turns out, and we will study this in more detail
in the next chapter (in CHEM 1515), that at a specific
temperature the amount of water in the vapor phase above a liquid
is known. This is called the vapor pressure of water. At around
25 deg. C the vapor pressure of water is approximately 24 mmHg.
So the total pressure of the gas sample collected is the pressure
due to the pure gas generated in the reaction and the pressure
due to water in the vapor phase.
PTotal(Patm) = Psample
+ Pwater
The ideal gas equation is an empirical relationship which
describes how an ideal gas behaves under a given set of
conditions, but it does not explain why gases behave as they do.
To try to explain the behavior of an ideal gas a model which will
enable us to image how gases behave at the atomic level is
needed. Such a model has been developed and is known at the
Kinetic-molecular theory for ideal gases. The model evolved over
a period of 100 years and is the product of the work of many
early scientists. The kinetic molecular model is based on the
following postulates;
Gases consist of tiny (submicroscopic) molecules
which are in continuous, random motion.
The distance between molecules is large compared with
the size of the molecules themselves. The volume occupied
by a gas consists mostly of empty space.
Gas molecules have no attraction for one another.
Gas molecules move in straight lines in all
directions, colliding frequently with one another and
with the walls of the container.
No energy is lost by the collision of a gas molecule
with another gas molecule or with the walls of the
container. All collisions are perfectly elastic.
The average kinetic energy for molecules is the same
for all gases at the same temperature, and its value is
directly proportional to the absolute temperature.
I have prepared a computer generated model to represent these
postulates. So lets study the computer generated model and see
how it behaves.