In Chapter 1 and 2 we will discuss in detail the three states of matter. Here
is a macroscopic view of each state and a microscopic
view.
If we look at a periodic table which identifies the phase of
each element at standard conditions we see that the dominate
phase is solid followed by the gas phase and finally the liquid
phase.
The elements which are gases include, hydrogen, helium,
oxygen, nitrogen, fluorine, chlorine and all the noble gases.
I'll expect you to know the standard state phase of every element
in the periodic table. Now you might be thinking, holy cow, are
you nuts, but remember 2 of the elements are liquids and 10 of
the elements are gases. So it is not so bad. Also I'll expect you
to know the color of each of the gaseous elements.
Under appropriate conditions substances which are normally
liquids or solids can exist in the gas phase. In such cases the
gaseous phase of the substance is called vapor. For example, one
of the two elements which exists as a liquid is bromine.
The three phases of matter differ very obviously from one
another. A gas is differentiated from other matter by two
characteristics: 1) it has no definite shape and 2) it has no
definite volume, but expands to occupy its container.
The liquid state has a definite volume, but no definite
shape. The liquid flows and when poured from one container to
another takes the shape of the container. Liquids have no
definite shape.
A solid does not flow but has a definite volume and shape. To
change the shape requires the application of considerable force.
Perhaps the most familiar property of a gas is its
compressibility. The properties of gases such as compressibility,
mixing and diffusion occur because of the large separation
between individual molecules. In the solid phase individual
molecules are very close together, while in the gas phase the
separation between molecules is very large.
So our goal in the first part of this chapter will be to
develop a quanitative understanding of how temperature, volume
and pressure effect the properties of a gas.
We'll begin with a discussion of pressure.
Pressure is a measure of the force of an object, or
collection of particles, on a given area. Another way of saying
the same thing, is pressure is the force exerted on an object
divided by the area over which the force is distributed.
Mathematically, we would write this relationship in the following
way;
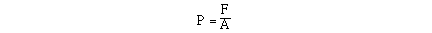
We need to make a distinction between pressure and force.
Something familiar to all of us is going down to the gas station
to pump up a bicycle tire. Tires require between 40 psi (pounds
per square inch) to 130 psi. We know adding more air to the tire
increases the pressure. The number of psi increase. The units
(psi) describe the weight exerted by the gas divided by the area
over which the weight is distributed. We also understand that P
is proportional to the number of moles of gas in a container.
The difference between force and pressure can be described in
terms of a person walking on a frozen lake. Up right, the person
weight (mass x gravity) is distributed over a small area
(area of shoes). If the ice is thin it may break as a result of
the person standing on it. By lying down, and lying flat on the
ice the individual's weight is distributed over a greater area
and the pressure decreases.
Atmospheric pressure is a term that should also be familiar
to you. The local weather report includes a map of the US with
indicated regions of high and low pressure. This suggests that
pressure is not constant. If we read the newspaper or watch a
weather report the pressure is stated and it changes each day.
You also know that at high altitudes (show an airplane)
the pressure is lower than on the ground.
We can measure the pressure exerted by the atmosphere by filling a hollow
glass tube with mercury, (a tube longer than 76. cm) and while plugging the
bottom of the tube inverting it into a pan containing mercury. (Note: the mercury
barometer was first developed by Evangelista Torricelli in 1643) Such a device
is called a barometer (
). The atmospheric pressure is obtained by
measuring the distance between the surface of the mercury in the reservoir and
the top of the mercury in the tube. Well you might ask, why didn't the mercury
run completely out of the tube when it was inverted into the pan? The answer
is the pressure exerted by the atmosphere supports the column of mercury. Another
way to describe this is the weight of mercury in a column 760 mm high is equal
to the weight of the air above the surface of the mercury in the pan.
Another device which can measure pressure of a small sample of a gas is a
manometer. (Show
a manometer) A manometer consists of a U-shaped tube, one end of which is
open to the atmosphere the other is in contact with a sample of gas of interest.
An open ended manometer is used to measure gas pressure near atmospheric pressure.
In the manometer mercury is in contact with the atmosphere and with the sample.
Knowing the atmospheric pressure and measuring the difference in height of the
two levels one can calculate the pressure of the sample of gas.
In the picture their is a sample of a colorless gas in the round-bottom flask.
The flask has been attached to a manometer. To measure the pressure of the gas
in the container the stopcock must be turned to allow the gas to be in contact
with the sample. When we open the stopcock we can see a change in the height
of the mercury in the manometer. In this case the level of the mercury on the
side in contact with the gas sample is lower compared to the level in contact
with the atmosphere. For this to happen the pressure inside the container must
be larger than atmospheric pressure. To determine the pressure inside the container
we use the relationship,
Psample = Patmosphere + (hatm - hsample)
Opening the other stopcock on the container holding the sample of gas so the
sample is in contact with the atmosphere we see the levels of the manometer
are equal. The pressure of the gas in the container equals atmospheric pressure.
If the height of the mercury column in contact with the gas sample is higher
than the level of mercury in contact with the atmosphere the same equation is
used. The result shows the pressure of the gas sample is lower than atmospheric
pressure. (Do two examples and have the students determine the pressure of the
gas sample.)
We can demonstrate the presents of atmospheric pressure by
the following simple experiment (
QuickTime movie, 1.6 M
file)(this version is displayed in a larger frame size/2.4 M file).
If a soda can is partially filled with water and the water heated
to boiling, nearly all of the air is swept from inside the can.
If the top of the can is quickly sealed and the water in the
vapor phase rapidly cooled a large difference in pressure is
obtained. This can be accomplished by inverting the can and
immersing it in a container of water at room temperature. . We
will discuss aspects of this experiment later in the lecture.
Area of the pop can is 2(pi)r(h + r) = 2(3.14)(1.125)(4.75+1.125)
= 32 in2. Pressure is 
so the weight of the atmosphere on the can
is 14.7(32) = 470 lbs.