The ideal gas equation is an empirical relationship which
describes how an ideal gas behaves under a given set of
conditions, but it does not explain why gases behave as they do.
To try to explain the behavior of an ideal gas a model which will
enable us to image how gases behave at the atomic level is
needed. Such a model has been developed and is known at the
Kinetic-molecular theory for ideal gases. The model evolved over
a period of 100 years and is the product of the work of many
early scientists. The kinetic molecular model is based on the
following postulates;
Gases consist of tiny (submicroscopic) molecules
which are in continuous, random motion.
The distance between molecules is large compared with
the size of the molecules themselves. The volume occupied
by a gas consists mostly of empty space.
Gas molecules have no attraction for one another.
Gas molecules move in straight lines in all
directions, colliding frequently with one another and
with the walls of the container.
No energy is lost by the collision of a gas molecule
with another gas molecule or with the walls of the
container. All collisions are perfectly elastic.
-
The average kinetic energy for molecules
is the same for all gases at the same temperature, and its value is directly
proportional to the absolute temperature.
I have prepared a computer generated model to represent these
postulates. So lets study the computer generated model and see
how it behaves.
You can see a region (a box) which constrains the particles
of gas. Although the particles are not particularly small for an
ideal gas we do see they are in continuous, straight line motion.
Again because of the computer, and to allow easy viewing the
particles are not widely spaced. Notice the particles are not
attracted to each other. The gas particles move in a straight
line between collisions. If we color one of the particles
differently than the others we can see the straight line motion
easier. The collisions are also easier to identify.
If you are observant you may see that the colored particle
has different speeds, sometimes fast, and sometimes slow. In this
computer model the number of different speeds is limited. An
important point must be made to identify the difference between
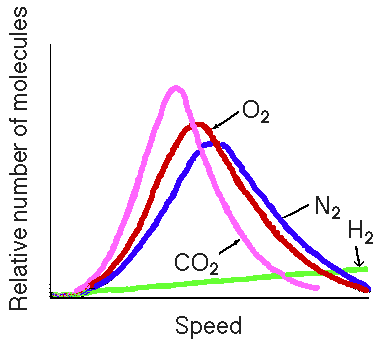
this computer simulation and reality. For an ideal gas there is a
much broader range of speeds of the particles. In fact a plot of
molecular speed and fraction of gas particles with a particular
speed is shown on the overhead. (Show overhead of molecular
speed distribution). Notice that at a given temperature there
are fractions of gas particles with very high speeds, and
fractions of particles traveling very slowly. As the temperature
is changed the speed distribution changes. If we increase the
temperature the curve shifts to higher speeds. The kinetic energy
of a collection of gas particles is given by
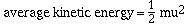
where m is the mass of a molecule of the gas and u is its
root-mean-square velocity. The root-mean-square velocity is not
exactly equal to the average velocity, but they are close. The
rms velocity is the speed of a molecule that has the average
molecular kinetic energy. This relationship will be important in
later discussions of some interesting properties of gases. Right
now it is important to recognize that a collection of gas
particles has a range of speeds, not a single speed.
When a collision occurs energy can be transferred. So if the
white gas particle is moving slowly and it collides with a fast
moving particle, transfer of energy can result in the white
particle moving faster, and the other particle slower after the
collision. Total energy of the collision is conserved--elastic
collision.
Now the usefulness of a model depends on its ability to
reproduce experimental observations as well as make predictions
which can be verified by further experiment.
Lets begin by verifing some of the experiments we performed
earlier. Boyle's Law related pressure to volume of an ideal gas
at constant mol and temperature. So if set the temperature at 300
K and 4 mol of gas we can observe how the pressure is effected by
a decrease in volume. Initially the pressure is 2.59 atm.
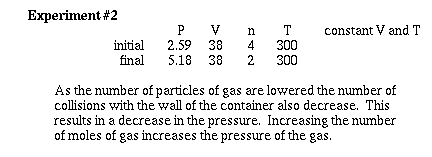
Lets observe what happens as the number of moles
of gas are changed at constant temperature and volume.
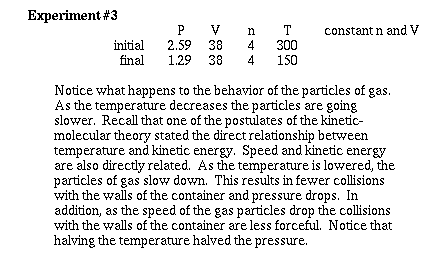
Now lets consider how changing the temperature
of a gas effects the pressure at constant volume and constant
moles. To help recognize how we use the Kinetic-molecular model,
watch carefully what happens as the temperature is lowered.
Now lets consider how changing the temperature
of a gas effects the volume at constant pressure and constant
moles. We will change to the 'V' mode to calculate volume. To
help recognize how we use the Kinetic-molecular model to explain
Charles' Law, watch carefully what happens as the temperature is
lowered.
Diffusion and effusion
The last postulate says the average kinetic energy for
molecules is the same for all gases at the same temperature. It
should be noted that this says if you have two samples of gas,
one with a large mass and one with a small mass, the average
speed of the sample with the large mass is slower than the
average speed of the light gas. For example, the average speed
for a collection of H2 molecules at 25 degrees C is
1766 m.sec-1, (2.55 x 104 miles.hr-1)
while for Cl2 it is 286 m.sec-1
(4.13 x 103 miles.hr-1).
The last postulate in the kinetic-molecular theory indicates
there is a direct relationship between kinetic energy and
temperature. We will not derive this relationship, but simply
state it as;
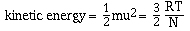
where R is the ideal gas constant (8.314 J.K-1.mol-1),
T is the absolute temperature and N is Avogadro's number. If this
equation is solved for velocity, u, we have;
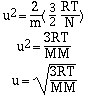
At a given temperature the velocity of a gas is inversely
proportional to its molar mass. This relationship helps us
understand two phenomena, effusion and diffusion. Effusion is the
rate of escape of a gas particle through a tiny hole, as when a
gas escapes from a balloon, and it depends on the molar mass of
the gas. Diffusion refers to the spread of a gas through another
gas, for example when perfume diffuses through a room.
For effusion the rate is directly proportional to the
velocity of the gas. The higher the velocity of the gas the
faster the gas effuses. Grahams law of effusion says the effusion
rate of gases are inversely proportional to the molar masses.
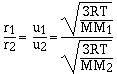
cancelling the constants
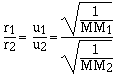
which is the same as
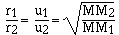
The explanation for rate of diffusion is more complicated
because of the effect of collisions with other molecules (these
collision are absent in effusion) but the net result is the same,
the rate of diffusion is identical to the rate of effusion.
The difference in the rate of diffusion due to the difference in mass is used
to separate the relatively low abundant uranium isotope 235U (0.7
%) from the more abundant isotope 238U (99.3 %). The uranium is converted
to the volatile UF6 which, while a liquid at room temperature, boils
at 56 degrees C. The sample of gas is allowed to diffuse through a porous barrier
from one chamber to the next. As a result in the small difference in mass of
the volatile compounds the lighter isotope concentrates after passing through
thousands of chambers.
Real Gases
Although ideal gas equation is a very useful description of gases, many gases,
most gases do not obey this relationship. Gases which do not obey the ideal
gas equation are call real gases.
To see how real gases
behave we will consider plotting the quotie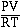nt 
versus P for the gas. For 1 mol of an ideal
gas a plot of this quotient as the pressure increase behaves as we see in the
figure below. According to Boyle's law increasing the pressure decreases the
volume. For an ideal gas the plot is a constant.
However, with real gases we observe deviation from this plot. Lets consider
carbon dioxide and observe how this quotient changes as we increase the pressure.
This is interesting.
How do we understand the observed behavior? For real gases we must consider
that two of the postulate of the kinetic molecular theory are not obeyed. These
are postulate 2. For ideal gases this postulate says the volume occupied by
the molecule is negligible compared to the volume of the container.
So let's look at it this way. As the pressure on a gas increases the volume
of the container decreases. As the volume of the container gets smaller and
smaller the volume available for the gas particles, decreases. Since real gases
do occupy some space the actual volume (free space volume) which is available
for the gas particles is smaller than the volume of the container. The result
is the product of PV is greater than it should be and we see this positive deviation.
This is most evident in hydrogen, put is present in carbon dioxide and nitrogen.
We also see that carbon dioxide and nitrogen exhibit a negative deviation initially.
This behavior is explained because these two gases deviate from the 3rd postulate
of the kinetic molecular theory. For ideal gases there are no attractions between
particles of the gas. For real gases this is not the case. As the pressure increases
the molecules are forced closer together. As the separation between molecules
decreases they experience attraction to adjacent gas particles. When this happens
the particles do not exhibit as greater a pressure as would be expected.
Imagine a particle approaching the wall of a container. When particles are
close together this approaching gas particle feels an attraction to neighboring
particles which decreases the force of the impact with the wall of the container.
As a result the real pressure is less than the ideal pressure. The product PV
is now less than is expected for an ideal gas and we observe a negative deviation.
The degree of the negative deviation is a good measure of the importance of
the attraction of particles in the gas phase to each other. That is hydrogen
exhibits no negative deviation. Attraction between particles is not important
for this gas, compared to carbon dioxide.
To account for these deviations the van der Waals equation is used. The form
of this equation is;
