The first property to explore is atomic radius. The immediate question is what is an atomic radius. Our quantum mechanical description of an atom suggests a very broad region for finding the electron. It is difficult to define a sharp boundary for distance between the electrons in any particular atom and the nucleus. So some approximations are made in determining this parameter. For example, the distance between the two chlorine atoms in Cl₂ is known to be 1.988 Å. To get the atomic radius we assume the distance between the two nuclei is the sum of two chlorine atomic radii. Therefore the atomic radius of chlorine is 0.994 Å. Additional distances can be obtained from other distances between atoms. Care must be taken in these types of determinations however.

After collecting large amounts of data generally accepted atomic radii are known for most elements in the periodic table. Atomic radii determine this way are also called covalent radii. (we'll discuss the term covalent in the next chapter) Atomic radii for metals can be estimated from the distance between metal atoms in the pure solids. Figure 11.32 in your text graphically summarizes the observed atomic radii for most elements.

Looking at the table notice from lithium to cesium, going down the group, the atomic radius increases. This is as expected as the valence electron is located further and further from the nucleus. Each of the elements in a group have the same number of valence electrons. In the case of Group I there is one valence electron. In lithium this single valence electron is found in the second level, in sodium the single valence electron is located in the third level. The third level is higher in energy AND further away from the nucleus. Therefore a sodium atom is larger than a lithium atom. The argument is the same for other higher members of the group.

Also notice that going across a period the atomic radius decreases. We can understand this trend by considering that as we go across a period each electron added is going into the same level. For example look at the electron configuration for the eight elements in the third period.

Na 1s²2s²2p⁶3s¹

Mg 1s²2s²2p⁶3s²

Al 1s²2s²2p⁶3s²3p¹

Si 1s²2s²2p⁶3s²3p²

P 1s²2s²2p⁶3s²3p³

S 1s²2s²2p⁶3s²3p⁴

Cl 1s²2s²2p⁶3s²3p⁵

Ar 1s²2s²2p⁶3s²3p⁶

Sodium has one valence electron and as we move across to argon with eight valence electrons. Remember, and this is important, the valence electrons are in the outer most level of the atom (the furthest from the nucleus). Remember also that as we move from sodium to argon, the nuclear charge, the number of protons in the nucleus, is also increasing. Sodium has 11 protons and argon has 18 protons. Each time we add a proton to a the nucleus the electron (which are negatively charged) feel a greater attraction to the nucleus. Since valence electrons are all in the same level, they feel a greater attraction to the nucleus as we move across the period. If the valencce electrons feel a greater attraction they are pulled in closer to the nucleus and the atom gets smaller. So the one valence electron in sodium feels a certain attraction to the nucleus. Magnesium has two valence electrons, both in the same level, and both of these electrons feel a greater attraction to the nucleus because the nuclear charge has increased from going from sodium to magnesium.

You might ask why doesn't the radius get smaller as we go from sodium to potassium? Potassium has a greater nuclear charge compared to sodium. You're right potassium does have a greater nuclear charge compared to sodium. The difference is the valence electron in potassium is in a different and HIGHER level compared to the valence electron in sodium. So the valence electron in potassium is further away and can not feel the higher nuclear charge. When going across a period each added electron goes into the SAME level. SInce the nuclear charge is also increasing the valence electron feel a greater attractio to the nucleus and the atom's size gets smaller.

Another important trend which is related to the periodic table is the ionization energy for an element. It is related to the energy required to remove an electron from an atom. Clearly a multi-electron atom would have many ionization energies. So by definition the first ionization energy is defined as the energy required to remove the outer most electron from a neutral atom in the gas phase. An equation can be written to show this definition,

M(g) -> M⁺(g) + 1e^-

The second ionization energy is the energy required to remove the next outer electron from the singly charged ion.

M+(g) -> M²⁺(g) + 1e^-

Subsequent removal of electrons can also be written and determined.

As you would expect each successive removal of an electron requires more energy. As electrons are removed the remaining electrons experience a greater attraction to the nucleus. As shown in the table the ionization energies increase with each successive removal. Notice that there occur major changes as successive electrons are removed. For magnesium there is a large change between the second and third electrons, for aluminum between the third and fourth, for silicon between the fourth and fifth. Magnesium has the electron configuration of 1s²2s²2p⁶3s². The first two electrons are removed from the third level. The third electron is removed from the second level. Electrons in lower levels feel a greater attraction to the nucleus and are more difficult to remove.

Looking at the table suggests the valence electrons, the outer most electrons, require considerably less energy to remove. This suggests that the outer electrons are much easier to remove from the atom compared to the inner level electrons. The inner level electrons are too tightly bound to be involved in chemical bonding.

TABLE Successive values of ionization energies (I) for the elements sodium through argon (kJ/mol)a

Now consider the variation in the first ionization potentials and position of the element in the periodic table. If we look at a plot of 1st ionization versus atomic number certain trends are evident. The figure below shows the 1st ionization energies.

Notice the general trend is for the ionization energy to increase going across a period. This makes sense if we recall the atomic radius decreases going across the period. If the atom gets smaller it means the electrons feel a greater attraction to the nucleus and it is more difficult to remove the electron.

When we look more closely at the trend in ionization energies we see two deviations. Boron's ionization energy is lower than beryllium's and oxygen's is lower than nirogen's. What gives? In the first case, lets look at the energy level diagram for boron and beryllium.

Notice the energy for the 2s and the 2p sublevels. The 2s sublevel is lower in energy compared to the 2p sublevel. So when we try to remove the first electron in boron it is easier because it is higher in energy. Therefore the the first ionization energy for boron drops when compared to beryllium. As we continue across to carbon and then to nitrogen the electrons are going into the same sublevel and we see the ionization energy increasing.

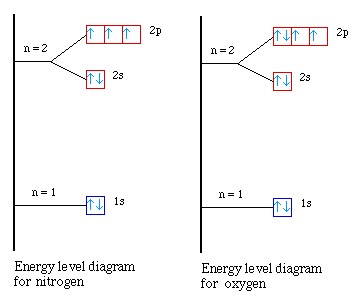
The second occurs from nitrogen to oxygen. What is going on in this case? Again we need to look at the energy level diagrams for the two atoms. In nitrogen all of the 2p orbitals are half-filled. When we go next to oxygen the electron must be placed in one of the half-filled orbitals. But we know that it requires some extra energy to place two electrons into the same orbital. Since it takes slightly more energy to pair the electrons it takes less energy to remove the paired electron in oxygen. So we see a small decrease in the first ionization energy when going from nitrogen to oxygen.