Analogies

  1. A mole (6.02 x 1023) is a counting number like dozen (12), gross (144), ream (500), etc. used to count objects such as eggs, pencils, or sheets of paper. Because atoms are so very small, measurements using ordinary laboratory-measuring equipment can only be made on very large numbers of them-on the order of Avogadro's number.
  2. Astronomers estimate that there is a mole (6.02 x 1023) of stars in the universe.
  3. Analogy to mole/mass/molecule calculations: Counting rolls of coins and determining the number of coins and their value is analogous to mole/mass/ molecule calculations, as the following activity suggests.
  4. Roll-Mole Analogy (by Caroline L. Ayers). As anyone who has taught chemistry knows, the mole concept is one of the most difficult in chemistry. The roll analogy was devised to show students that calculations involving moles are similar to some they can easily do-calculations involving money. Any student can do relatively complex calculations if they involve money.

    The Roll-Mole Worksheet (which follows) is designed to be used by answering Problems 1, 2, 1', and 2' first. Then have students fill in the blanks on the equalities. After this point, students are told to "forget" that a nickel is worth 5 cents and a quarter is worth 25 cents. They must not use that information in solving Problems 3 through 6 or the purpose of the exercise is defeated. (Nobody remembers the mass of an atom of an element or a formula unit of a compound!) The worksheet points out the information students are allowed to use to solve the problems. To use the worksheet most effectively, work Problem 3 and 3' side-by-side on the board so students see that the reasoning is identical. Students should be made aware of the reasoning (use a set up) for each


    problem so that they will recognize that moles are not really impossible to work with-Avogadro's number is just too large to picture. Students resist setting up the money problem. They say they do not know how they do it, they just do it. That is because such calculations are so familiar and thus easy to do. If they cannot tell what the set up should be, tell them and write it down, including units so they can see the units cancel out just as in the corresponding mole problem. Work Problems 4 and 4' together, etc. In the analogy, value ($) is like mass (g), number of coins is like number of atoms, and rolls of coins are like moles of atoms. (Note that "roll" rhymes with "mole".)

    4. Empirical Formula Analogy (by Kerro Knox, 1980)

    Given the average mass (weight) of boys and girls in a class and the percent boys by mass and percent girls by mass, calculate the ratio of boys to girls and the "formula" for the class (BxGy).

    Assume 100 kg of the class. The class would be 66.7% x 100 kg = 66.7 kg boy (B) and 33.3% x 100 kg = 33 kg girl (G).

    Formula for the class = B3G2

  5. Analogies to illustrate the size of Avogadro's number
    1. One mole of high school textbooks would cover the USA to a depth of about 320 km (200 miles).
    2. Water flows over Niagara Falls at about 650,000 kL (172,500,000 gallons) per minute. At this rate it would take 134,000 years for one mole of water drops (6.02 x 1023 drops) to flow over Niagara Falls.
    3. Avogadro's number (6.02 x 1023 ) is the approximate number of milliliters of water in the Pacific Ocean (7 x 108km3 or 7 x 1023 mL). (Analogy by M. Dale Alexander, Gordon J. Ewing, and Floyd T. Abbott, 1984.)
    4. If one mole of particles the size of sand grains were released by the eruption of Mount St. Helens, they would cover the entire state of Washington to the depth of a ten-story building. (Analogy attributed to Glenn Crosby.)
    5. Analogies by A. Truman Schwartz and Lucy T. Pryde:

      One mole of marshmallows would cover the USA to a depth of 105,000 km (6500 miles). NOTE: The volume of a marshmallow is estimated as 16 cm3 (1.0 in3 ). The area of the USA is 9.32 x 10 6 km2 or 3.6 x 10 6 mi 2.

      If an Avogadro number of pennies were distributed evenly among the 4.9 x 109 human inhabitants of earth, each man, woman, and child would have enough money to spend a million dollars every hour-day and night-and still have over half of it unspent at death.

      One guacamole is the amount of taco chip dip that can be made from an Avogadro number of avocados-plus appropriate quantities of tomatoes, onions, and chili. A train stretching to the North Star and back 2-1/2 times would be required to transport one guacamole. NOTE: This assumes that the volume of one standard avocado (pit removed) is 278 cm 3 and that other ingredients make up 25% of total volume. The average coal car has a capacity of 110 kL (4000 ft 3 ) and is 16 m (53 ft) long. The North Star is 680 light years distant.

      Suppose the Greek god Zeus, after observing the Big Bang 15 billion years ago, became bored and decided to count one mole of atoms. Zeus is omnipotent. He can count very fast (one million atoms per second) and, of course, never sleeps. He has currently completed over three-fourths of the task, and will be finished in just another four billion years.

      One mole of moles (animal-type), placed head to tail, would stretch 11 million light years and weigh 9/10 as much as the moon. NOTE: Each mole is assumed to be 17 cm long with a mass of 100 g. Speed of light = 3.0 x 10 8 m/s. Mass of moon = 6.7 x 1022 kg..

      One mole of marbles, each 2 cm in diameter, would form a mountain 116 times higher than Mount Everest. The base of the marble mountain would be slightly larger than the area of the USA. NOTE: Marbles are assumed to have hexagonal closest packing and the mountain has a cone of angle 30 degrees;. Area of USA = 9.32 x 106 km2.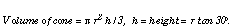

      TABLE OF CONTENTS TOPIC OVERVIEW CONCEPT/SKILLS DEVELOPMENT LINKS/CONNECTIONS EXTENSIONS