Chapter 13

Colligative Properties

Having discussed concentration units we need to extend the idea of solutions to investigate how some physical properties of the solvent are effected upon addition of a nonvolatile solute. A nonvolatile solute is a solute which has little tendency to escape from the solution. A solution of a nonvolatile solute (solid) has properties that are modified from the properties of the liquid (solvent). The difference between the properties of the solution and those of the pure liquid are a consequence of the number of solute particles present in the solution. The properties which depend on the number of particles of solute are called colligative properties.

These include;

1) Vapor Pressure lowering
2) Boiling Point elevation
3) Freezing Point depression
4) Osmotic Pressure

Colligative properties are properties which depend on the number of molecules or ions of solute present, and not on what the particles are (as long as they are not volatile). We will find colligative properties are important as they will provide us with information about the number of particles of solute present, and hence about molecular weights and degree's of dissociation (ionization) in solution. Early chemists, such as Arrhenius, were able to show that for some solutes more particles were present in solution than there were 'molecules' of solute, and hence that the solute particles were breaking (dissociating) into ions.

To understand the effect of a solute on the physical properties of a liquid we will begin with what happens to the vapor pressure of a pure liquid upon addition of a solute. A pure liquid, at a given temperature will be in equilibrium with its vapor. If we consider water at 25 ûC, the vapor pressure is 23.6 Torr. If we prepare solutions, by adding a nonvolatile solute, containing different mole fractions of solvent as shown below, and measure the vapor pressure due to water above the solution, we would obtain the following data.

Graphing this data the plot looks like;

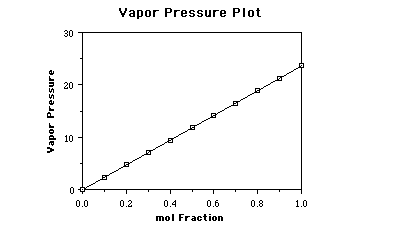
This is called Raoult's Law and is given as;

where;

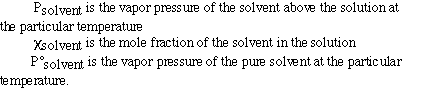
Here is a sample problem using Raoult's law;

The equation;

can be rewritten in a slighlty different form to suggest another useful technique. The mole fraction of solvent is given as;

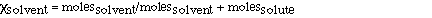
Which can be further transformed to;

From this relationship it is possible to determine the molar mass of a compound from the change in vapor pressure of the solvent.

The total vapor pressure above a solution is the sum of the vapor pressures of the solution components (solute and solvent).

Substituting for Raoult's law we have;

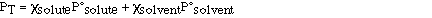
The composition of the vapor is not the same as the composition of the solution. Remember vapor composition, while it does depend on the mole fraction of the component of the solution also depends on the vapor pressure of the components. The vapor above a solution is always richer in the component that has the higher vapor pressure at the given temperature.

How the nonvolatile solute effects the vapor pressure of the pure liquid can now be transferred to the phase diagram to help us understand how the boiling point and melting point of the solvent are changed. If we select a point on the liquidÐvapor equilibrium line of the pure solvent we can read a particular vapor pressure. If a nonvolatile solute is added we know the vapor pressure is lowered by an amount that depends on the concentration of the solute particles present. So for the solution the liquidÐvapor equilibrium line is below that of the pure liquid. If we continue along the liquidÐvapor line for the pure liquid we continue to plot a new line for the solution. As we approach the boiling point, which occurs when the vapor pressure is 760 mm and we added some nonvolatile solute the vapor pressure drops. The solution stops boiling. To get the solution to boil we must increase the temperature of the solutionÐÐthe boiling point of the solution is higher than that of the pure liquid. The boiling point is elevated by the addition of a nonvolatile solute.

When we consider the effect on the melting point of the liquid we must recall that melting occurs at a temperature when the pure liquid is in equilibrium with the pure solid. In a solution, the liquid contains some solute, which does not crystallize in the pure solvent solid structure. So not every molecule that collides with the pure solid solvent is a solvent particle, however, every molecule that melts is pure solvent. So more molecules are melting, going into the liquid phase, than are solidifing. Inorder to reÐestablish the equilibrium the temperature of the solution must be lowered. At the lower temperature the solvent particles are moving slower and are more likely to solidify. The result is that the melting point of the liquid is depressed by the addition of a nonvolatile solute.

Now let's consider the boiling point and the freezing point of the solution. Let's look at the phase diagram for water. We know the location of the normal boiling point and the normal freezing point for water on the phase diagram. If we plot the liquid vapor equilibrium line for a solution of constant concentration (mol fraction) the new vapor pressure curve of the solution looks like this.

The resulting solution has a new freezing point which lower than the original freezing point. When the liquid freezes only the solvent molecules are formed in the solid, so no new solid-vapor equilibrium line is formed. The freezing point of the solution is depressed below the normal freezing point.

If we turn our attention to the boiling point of the solution we see the normal boiling point is elevated as a result of the solute. We can understand the boiling point elevation in the following terms. At the normal boling point of the pure solvent the vapor pressure is equal to the atmospheric pressure. If a solute is added the vapor pressure is lowered. In order for the solution to boil the temperature must be increased to increase the vapor pressure of the solution until it again equals atmospheric pressure.

It turns out that for dilute solutions of nonvolatile solutes the T_fp and the T_bp are proportional to the molality of the solution.

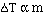
to get an equality we add a constant and

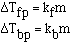
The magnitude of the constants are different for a particular solvent and also vary with different solvents. The units on 'k', the freezing point constant or the boiling point constant, are degrees C m^-1. For water the freezing point constant is 1.86 degrees C m^-1 and the boiling point constant is 0.512 degrees C m^-1. A 1 molal aqueous solution of any nonvolatile nonelectrolyte boils at 100.512 degrees C and melts at Ð1.86 degrees C. So if we have a concentration of a nonvolatile solution other than 1 molal we can use either equation to calculate the new boiling or freezing point. It must be remembered that when solving for ÆT that if the freezing point is expected the ÆT must be subtracted from 0 degrees C (freezing point depression) and added to 100 degrees C (boiling point elevation).

Another sample problem;

We can also use the expression to determine the molecular weight of an unknown solute. If we recognize that;

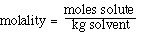
and that;

substituting into the freezing point expression we have;

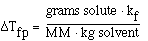
rearranging and solving for MW we have;

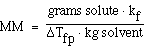
Another more interesting example;

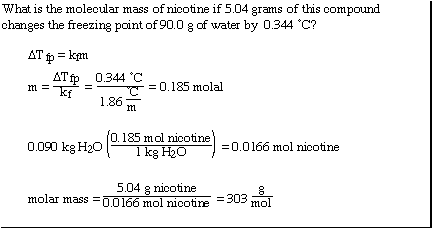
We can also use the colligative properties to help understand the behavior of strong electrolytes as well as nonelectrolytes. If we look at some experimental freezing point data some interesting information can be obtained.

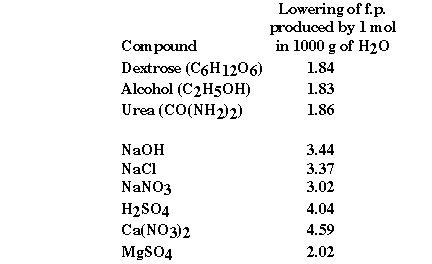
What is it about the second group of compounds that would explain the observed freezing point depressions? They are all ionic compounds! They are what we have called strong electrolytes, because we understand these compounds to completely dissociate in aqueous solution. But do they?

Experimentally the T_fp for NaOH is 3.44 degrees C. Ideally we would expect that all of the NaOH would dissolve according to the reaction:

NaOH(s) ÐH₂O--> Na⁺(aq) + OH^-(aq)

When an ionic compound dissolves in water the ionic compound exists as ions in solution. 1 mol of NaOH dissolves to form 2 moles of ions (particles). Inorder to deal with this behavior we need a variation on the freezing point expression. It is;

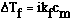
where;

Ideally we would predict that NaOH would completely dissociate so that 'i' would have a value of 2 and the theoretical freezing point would be 3.72 degrees C. We experimentally observe that all the NaOH dissolves yet the freezing point depression data suggest that not all of the NaOH has dissociated. Some of the NaOH remains associated. Based on the experimental change in freezing point the experimental value of 'i' is 1.85. In general, the more concentrated the solution the greater the observed deviation from ideality. As the solution becomes more dilute the experimental 'i' value approaches the theoretical value. The difference between the ideal value of 'i' and the observed is due to something we call ion-pairing. In an aqueous solution the ions of the solute are surrounded by water molecules. If the the solution is very dilute the large number of water molecules that surround the ions effectively prevent the ions from seeing each other. All an individual ion sees is water molecules. At higher concentrations of ions the number of water molecules available for solvation is lowered and there are fewer water molecules surrounding any particular ion. The result is the ions can 'see' each other and they feel some attraction and they will 'pair up' in solution. When they pair there are fewer particles in the solution and 'i' drops from it ideal value.

We can use experimental 'i' values obtained by measuring the freezing point depression of electrolytes to determine whether the substance is strong, weak or a nonelectrolyte. For example, when the freezing point of a 0.100 molal solution of HCl is measured the observed value is 0.353 degrees C. Is HCl an electrolyte? If it were not the expected change in temperature would be 0.186 degrees C. Based on our experimental data HCl is in fact a strong electrolyte and is 90 % dissociated. On the other hand a 0.100 molal solution of HC₂H₃O₂ has a Tf of 0.195 degrees C, very close to 0.186 degrees C. Acetic acid is considered to be a weak electrolyte, while dextrose and urea are considered to be nonelectrolytes. With more understanding of this kind of problem we would be able to calculate the percent dissociation of the compound.