Bohr was suggesting the energy of the electron was quantized, that is the electron could only exist in certain allowed energy levels.

In order to reproduce the same equations determined empirical by Rydberg and the others, Bohr formulated a model of the hydrogen atom where the electron could only occupy certain energy states called stationary states.

Bohr's mathematical relationship which expressed these ideas is;

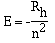
Note R_h is = 2.18 x 10^-18 J. The negative arises because Bohr assumed that when the electron is removed from the atom the system would be defined as having zero energy. But when the electron is around the nucleus, the system is more stable and therefore, must be at a lower energy. Therefore, the negative sign. 'n' in the equation is a special number called a quantum number. It can only have integer values from 1 to infinity. The quantum number is also a way of labeling each orbit available to the electron. The first orbit is referred to as the ground state, or the state of the atom at its lowest energy.

The equation suggested by Bohr can generate the equation obtained by Rydberg and the others by recalling,

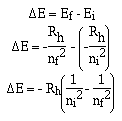
Bohr was also able to calculate the radius of the electron in each of the allowed orbits. These are given by the equation,

r = n² (5.30 x 10^-11 m)

If the energy values of the first 10 orbits are calculated one can see the energy gets closer and closer to zero, and the energy of the orbits as n get larger get closer together. This can best be seen when the energies are plotted on a graph. Simultaneously the radius of the orbit of the electron gets larger and larger. So as the electron gets further away from the nucleus the energy of the electron inthe orbit gets closer to zero.

So if we plot the energy levels for the electron in the hydrogen atom we have a series of levels that look like;

Note as n increases the difference in energy between subsequent levels gets smaller while the separation between energy levels gets larger. The radius can be though of as the distance of the electron, in the particular energy level, from the nucleus. The electron can occupy any of these energy levels, which are further and further from the nucleus. Bohr's model can now be used to explain the observed emission spectrum for hydrogen. To do this Bohr postulated that the electron could change energy only by going from one energy level to the next. Such a change was called a transition.

The absorption and the emission spectrum of hydrogen could now be explained in the following way. If the electron is in the ground state of the atom and a photon of light of the exact correct frequency (energy) is incident on the atom the electron can absorb the energy of the photon and is excited to a higher energy level, or higher orbit. Later the electron can fall from the orbit of high energy back to the ground state by re-emitting the photon of light of the same frequency as the original photon which excited the electron. For example, if an electron were in the n = 2 energy level and fell to the n = 1 energy level the difference in energy is;

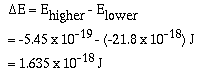
Recall that,

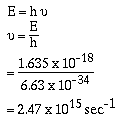
The same value for the first line in the Lyman series of the emission spectrum of the hydrogen atom. The photon that is released in this transition from the n = 2 level to the n = 1 level has a frequency of 2.47 x 10¹⁵ sec^-1. So the electron falling from any energy level to the n = 1 level reproduces the Lyman series of lines in the emission spectrum of the hydrogen atom. An electron falling from any level to the n = 2 level, reproduces the Balmer series, etc. Remember for the electron to go from a lower energy level to a higher energy level an absorption of energy must occur. But to make the particular transition it must absorb a photon of the exact energy. No more, no less.

When an electron moves from one energy level (stationary state) to another it either absorbs energy or emits energy. When it is in any of the energy levels it does not spontaneously emit energy and spiral into the nucleus.

As accurate as Bohr's model of the atom was in reproducing the discrete lines in the emission spectrum of the hydrogen atom, there was still a problem. As spectroscopic techniques were refined and developed, faint new lines began to appear in the emission spectrum that began to severely tax Bohr's model. In addition, it was shown that Bohr's model we unsuccessful in explaining the emission spectrum of the next element in the periodic table-helium. Bohr's model of the atom was simple, but it is incomplete. What is required is a new and different way to thing of the atom to better understand the messages it is sending us.

Bohr's model worked for a simple system, but did not completely explain additional detail associated with the emission spectrum. To a point it worked. In these circumstances modifications of the model are typical needed. The primary modification of the Bohr model which resulted in our current view of the electronic structure of the atom was to recognize the electron exhibited wave properties as well as particle properties. This rather simple statement was the result of considerable labor. Let's go back to the origin of the ideas which subsequently lead to this important modification of describing the behavior of an electron in an atom.

In his study of the Photoelectric effect Einstein recognized that light exhibited particle behavior. When light of specific frequency was incident on a metal surface electrons were ejected from the metal. The incident light in causing electrons to be ejected was behaving as a particle. Light, electromagnetic radiation, could not only be thought of as having wave properties, but also particle properties. A packet of light (photon) had a frequency, but it also had an energy given by;

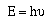
Now we began paying a price for our search to elucidate the structure of the atom and a gentleman by the name of Louis Victor de Broglie is responsible. What he did was to make the atom an abstract and and difficult to imagine. He made the universe probabilistic and indeterminate. Now understand that the universe has not changed, but our view of it has.

The pivotal concept suggested by de Broglie, was that if light could exhibit particle properties, and therefore, help us explain phenomenon, then why could not matter have wave properties. de Broglie was saying that matter, under certain circumstances might also display appreciable wavelike properties. He suggested that the wavelength of matter behaving in this manner could be calculated using the relationship;

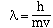
where 'm' is the mass of the particle and 'v' is its velocity.

Called matter waves they should not be confused with the waves of electromagnetic radiation. Matter waves are not radiated into space or emitted by a particle; they are never dissociated from the particle. The speed of matter waves is never the speed of light, nor is it constant, but changes with the particle. de Broglie suggested that electrons, because of their very small mass and high velocity, could behave as waves. There existed experimental evidence to support this idea. Even Thomson had observed the beam of electrons in the cathode ray tube would cast a shadow on the end of the tube when a piece of metal is placed in the beam.

For years after de Broglie's postulate Clinton Davidson and L. Germer investigating the scattering of electrons by atoms in a crystal showed that the electron beam was reflected (diffracted) in an identical way that X-rays were diffracted. Exhibiting the wave-like character of the electron. Erwin Schrodinger, an Austrian theoretical physicist, assumed that the wavelike character of the electron could be incorporated into a model of the atom. And here is where our world falls apart, and it becomes very difficult to describe electron behavior in atoms. Because now the medium has turned form pictures to probability and quantum mechanics or wave mechanics. The language is differential calculus, the words are symbols and numbers. The results are complex, but nonetheless dramatic.

We will avoid that pit and try to describe the results. Try is what I will do, because quantum mechanics changes the way we think about the motion of particles as small as the electron. Large objects moving slowly are easy to follow. Like a baseball. A propeller turning slowly is also easy to follow, However, as we speed up the blade it becomes difficult to know exactly where the two ends of the propeller are located. Their movement describe a region where, if we were to insert a pencil, we would expect to encounter one end of the blade or the other. Outside its length we would assume we would be safe. In the world of the atom the motion of the electron is equally complex. It can be thought of as smoothed out around the nucleus. We can not see an individual electron or how fast it is going.

Werner Heisenberg showed by using quantum mechanics that it is impossible to know both the position and velocity of the electron;

Now this problem is only encountered in the realm of the atom, we do not have such problem in the macroscopic world. (If we did more of us would pay closer attention to the 'walk' and 'don't walk' sign at traffic signals). Heisenberg's uncertainty principle says that because of the wavelike character of the very small electron we can not know precisely where the electron is when traveling along a path or trajectory.

If we accept that an electron has wave character than an electron can be described as a wave. If we use a single wave to decribe the velocity of the electron, as shown in the example, we do not know where the electron is located exactly. We have an idea of its vertical location, between the peak maxima, but we do not know where it is located horizontally. If we use a number of different waves and add them together we can better locate the position of the electron, but we have no idea what the velocity of the electron is because of the different velocities of the waves that contribute to the electron. So Heisenberg's uncertain principle concludes that we can not know both the position and the velocity of an electron simultaneously. This means we can not know exactly where the electron is an any instant.

We can not know how fast an electron moves in an atom (about the nucleus). However, quantum mechanics does allow us to describe the behavior of the atom in a statistical sense. We talk about the probability of finding the electron at a certain point in space in the vicinity of the atom. We can not describe the electron as orbiting the nucleus. Because to do so suggests the electron has a trajectory which suggests we can know both the position and velocity of the electron. So in quantum mechanics we describe the behavior of the electron in three-dimensional terms. Instead of finding an electron in an orbit, as Bohr's model suggested, we describe the electron in an orbital, which is a 3-dimensional orbit. But now the question becomes what 3-dimensional shape or shapes does an electron in a hydrogen atom have?