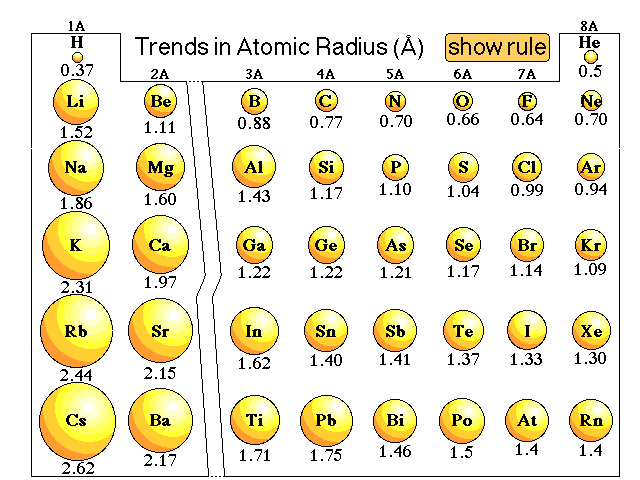
Explanations of trends in atomic radii that do not work perfectly:We might argue that going from hydrogen through the elements that the number of electrons increase. Since electrons repel each other due to the like charges, and the size of the atom will increase. The more electrons the larger the atom. We might be able to use that argument to explain the trend within a group, but when we look at the atomic radius trend going across a period the radius decreases.So we could argue that going from hydrogen through the elements the number of protons increases. Since electrons are attracted to protons we might expect that the more protons the smaller the radius. That might explain the trend in atomic radii going across a period but it does not explain the trend going down a group. Cesium has a large number of protons, yet it is one of the largest atoms, not the smallest.Here is our lecture discussion on this issue. |
Element |
Nuclear
|
Electron
|
Inner Core
|
Valence
|
Effective Nuclear
|
Na |
11 |
1s22s22p63s1 |
10 |
1 |
+1 |
Mg |
12 |
1s22s22p63s2 |
10 |
2 |
+2 |
Al |
13 |
1s22s22p63s23p1 |
10 |
3 |
+3 |
Si |
14 |
1s22s22p63s23p2 |
10 |
4 |
+4 |
P |
15 |
1s22s22p63s23p3 |
10 |
5 |
+5 |
S |
16 |
1s22s22p63s23p4 |
10 |
6 |
+6 |
Cl |
17 |
1s22s22p63s23p5 |
10 |
7 |
+7 |
Ar |
18 |
1s22s22p63s23p6 |
10 |
8 |
+8 |
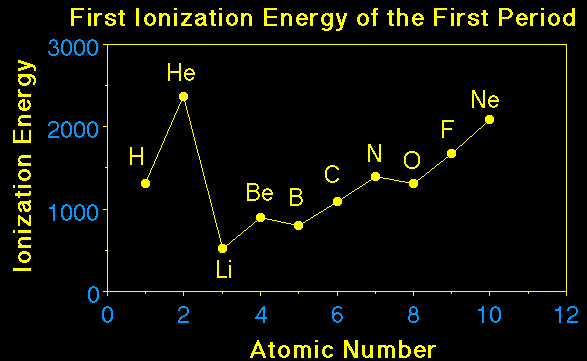
How would we explain why the atomic radius of a phosphorus atom is smaller than the atomic radius of a magnesium atom?How would we explain why the atomic radius of a sodium atom is smaller than the atomic radius of a cesium atom?Here is the explanation from lecture. |
![]()
Element |
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
I7 |
Na |
490 |
4560 |
|||||
Mg |
735 |
1445 |
7730 |
||||
Al |
580 |
1815 |
2740 |
11,600 |
|||
Si |
780 |
1575 |
3220 |
4350 |
16,100 |
||
P |
1060 |
1890 |
2905 |
4950 |
6270 |
21,200 |
Element |
Electron
|
Electron
|
Inner Core/
|
Effective
|
Na |
1s22s22p63s1 |
3s |
1s22s22p63s1 |
+1 |
Na+ |
1s22s22p6 |
2p |
1s22s22p6 |
+9 |
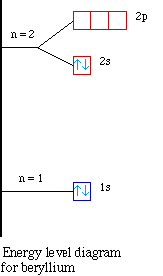
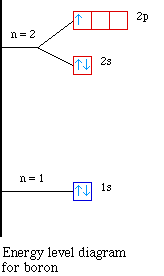
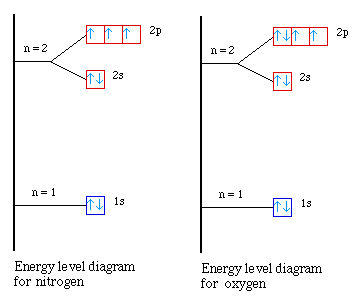
Nuclear Charge |
Element |
Electronic Configuration |
Effective Nuclear Charge |
Valence Electrons |
Core Electrons |
11+ |
Na |
1s22s22p63s1 |
1+ |
1 |
10 |
11+ |
Na+ |
1s22s22p6 |
9+ |
8 |
2 |
8+ |
O |
1s22s22p4 |
+6 |
6 |
2 |
8+ |
O2- |
1s22s22p6 |
+6 |
8 |
2 |
9+ |
F |
1s22s22p5 |
7+ |
7 |
2 |
9+ |
F- |
1s22s22p6 |
7+ |
8 |
2 |