Calculate the final temperature when a 136 mL of H₂O at 25.0 C is mixed with 75.0 mL of H₂O at 82.0 C.

Solution:

The important thing to remember here is when the two samples of water are mixed the sample at the higher temperature will transfer heat to the sample at the lower temperature. We can write this mathematically as,

q_{hot water} = -q_{cold water}

The amount of heat transferred is determined by the equation;

q= S.H. * mass * 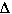T

So substituting this relationship into the first equation we get,

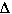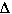S.H._{hot water} * mass_{hot water} * T_{hot water = - S.H.cold water * masscold water * Tcold water}

Now we simply substitute the information we know, (remember the density of water is 1.00 g mL^-1

1.84 J·g^-1C^-1 * 136 g * 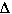T_{hot water} = - 1.84 J·g^-1C^-1 * 75.0 g * 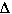T_{cold water}

This can be reduced to,

1.81 (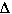T_{hot water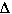}) = - T_{cold water}

Remember that,

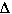T = T_final - T_initial

Therefore,

1.81 (T_final - T_initial)_hot = - (T_final - T_initial)_cold

Substituting;

1.81 (T_final - 25 C)_hot = - (T_final - 82.0 C)_cold

1.81T_final - 45.25 = - T_final + 82.0 C

2.81T_final = 127.2

T_final = 45.3 C