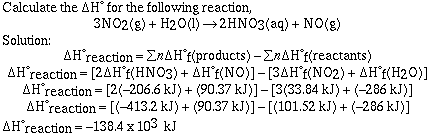We have discussed how we use calorimetry as an experimental method to determine the heat released or absorbed by a chemical reaction. I demonstrated both the coffee-cup and the bomb calorimeter. The coffee-cup calorimeter measures the heat released or absorbed in a reaction occuring in aqueous solution. I did one example showing how to calculate the heat of a reaction knowing the temperature change, the mass of the water and the heat capacity of the calorimeter. The bomb calorimeter measured the heat released in a combustion reaction. Bomb calorimeters are used to measure the heat of a reactions involving gases.

I made two important points during the lecture which I did not dwell on then, but which I want to re-iterate now. There is an important difference in the heat transferred in the two different types of calorimeters. The coffee-cup calorimeter measures the heat of a reaction at constant pressure, while the bomb calorimeter measures the heat of a reaction at constant volume. Our goal today is to introduce two important thermodynamic quantities, E, the internal energy and the energy associated with a reaction at constant volume and H, the enthalpy, the energy associated with a reaction at constant pressure. Introducing and discussing these two quantities is important to reaching our goal of calculating heats of chemical reactions.

In our calorimetry calculations and in several of the problems in PS10, we take advantage of the 1st Law of Thermodynamics, that energy is conserved. Energy that was lost by the system, in an exothermic reaction, was absorbed by the surroundings (the water and the calorimeter). Now we'll take a moment to apply some of these concepts in the first law of thermodynamics. The first law states that while energy can be converted from one form to another, it can not be created or destroyed. When a chemical reaction occurs energy lost by the system must be gained by the surroundings, and visa versa. This is also known as the law of conservation of energy.

The energy we are discussing is the sum of all the kinetic and potential energies of the systems component parts. This includes the motion of the atoms, or molecules, electrons and nuclei. This total energy is called the internal energy of the system. We use the symbol, E, to represent the internal energy of a system. The exact amount of the internal energy can not be determined. However, we can measure the change in internal energy of the system by measuring changes in temperature. For any physical or chemical change the change in internal energy is given as, (In chemical reactions the initial state is the reactants and the final state is the products. )

E = E_final - E_initial E = E_products - E_reactants

According to the first law

E_system +E_surroundings = 0

or

E_system = -E_surroundings

An important point is the sign of E. If E is positive that means the E_final is greater than E_initial. If E is negative it is the reverse.

In a chemical equation we can locate the internal energy depending on whether the reaction is endothermic or exothermic. For example, consider the reaction between dihydrogen and dioxygen to produce water;

2H_2(g) + O_2(g) ---> 2H₂O_(g)

This reaction is exothermic so heat would be located in the products;

2H_2(g) + O_2(g) ---> 2H₂O_(g) + heat

We can draw a representation of this reaction. In the diagram the internal energy of the reactants is greater than the internal energy of the products. When the reaction proceeds from reactants to products energy is released (we saw it). This is characteristic of an exothermic reaction.

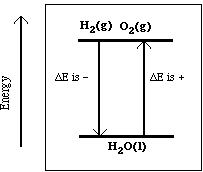
Another reaction, which we did in class, is described in the chemical equation;

Ba(OH)₂^.8H₂O_(s) + 2NH₄Cl_(s) ---> BaCl_2(aq) + 2NH_3(g) + 10H₂O_(l)

Recall this reaction was endothermic, so heat is located on the reactants side of the reaction.

heat + Ba(OH)₂^.8H₂O_(s) + 2NH₄Cl_(s) ---> BaCl_2(aq) + 2NH_3(g) + 10H₂O_(l)

In the diagram below the reactants are lower in energy compared to the products. As the reaction proceeds energy must be added. Notice the separation between reactants and products is different in the two diagrams. The separation is directly related to the magnitude of the change in the internal energy.

By definition if the system givens off heat, exothermic, E is -. If heat is absorbed by the system E is +.

According to the first law of thermodynamics a particular chemical system can transfer energy with it surroundings in the form of heat or work. Energy is transferred by adding or removing heat, or by doing or having work done on it. So when a system undergoes a chemical or physical change, the change in internal energy is given by the heat added to the system plus the work done on the system. The equation is,

E = q + w

There are many kinds of work, but in the chemical systems we are interested mechanical work done by expanding gases is the way reactions can do work. (Recall that expanding gases, from the combustion of gasoline, do work on the piston which eventually turns the wheels.)

w is PV for expanding gases

When a reaction system is open to the atmosphere the reaction does work on the surroundings, this is expressed;

as w = -PV

Work done by the system on the surrounding has a negative sign by convention. Reactions performed in the open atmosphere do work on the atmosphere, but this type of work by a system does nothing in a practical sense.

If in a chemical reaction the work done is accomplished by expansion then we can substitute for w in the equation; E = q + w

yields,

E = q - PV

so the change in internal energy for a system can be determined by measuring the heat transferred in the reaction and calculating PV.

If the chemical reaction occurs in a device which the volume of the reaction is held constant, then V = 0 and the change in internal energy is equal to heat transferred in the reaction. Recall for the reaction done at constant volume in the 'bomb' calorimeter we would expect V to equal 0. So under these conditions

q_v (constant volume) = E

So any heat gained or lost is equal to the change in internal energy.

If we perform a chemical reaction at constant volume and can measure the heat transferred in the reaction we can calculate E for the reaction.

What happens if we perform the reaction at constant pressure rather than constant volume? This is the case of most chemical reactions performed in the laboratory. In the case of a reaction open to the atmosphere the pressure is constant, not volume. We begin with our original statement of the first law,

E = q -PV

and define q as q_p the heat transferred at constant pressure.

E = q_p - PV

or

q_p (constant pressure) = E + PV

q_p the heat evolved or absorbed at constant pressure and is very important for most chemical system. The reactions we study in the laboratory are at constant pressure. q_p is called enthalpy and written as H (enthalpy).

H = q_p = E + PV

The heat flow at constant pressure, q_p, can be measured using a coffee-cup calorimeter. The reaction is performed in the water in the calorimeter and heat is absorbed or given up by the water and the calorimeter.

When a reaction is run at constant pressure open to the atmosphere it is difficult to calculate PV. Recall that according to the ideal gas law (PV = nRT) we can substitute nRT for PV. nRT is calculable from the information provided. n is equal n_{products gases} - n_{reactants gases}, R has the value of 8.314 J^.mol^-1.K^-1 and T is the temperature in Kelvins.

If the enthalpy of the products is greater than the enthalpy of the reactants H is positive, the reaction is endothermic. On the other hand when the enthalpy of the reactants is greater than the enthalpy of the products H is negative, the reaction is exothermic. For the reactions I demonstrated earlier, H = - 286 kJ (1/2H₂ + O₂), and +167 kJ (Ba(OH)₂ + NH₄SCN).

We can write the chemical equation as,

1/2H_2(g) + O_2(g) ---> H₂O_(g) + 286 kJ

or

1/2H_2(g) + O_2(g) ---> H₂O_(g) H = -286 kJ

167 kJ + Ba(OH)₂^.8H₂O_(s) + 2NH₄Cl_(s) ---> BaCl_2(aq) + 2NH_3(g) + 10H₂O_(l)

or

Ba(OH)₂^.8H₂O_(s) + 2NH₄Cl_(s) ---> BaCl_2(aq) + 2NH_3(g) + 10H₂O_(l) H = 167 kJ

We need to consider four important properties when using enthalpy in chemical reactions.

1. Enthalpy is an extensive property

   • The magnitude of H depends directly on the amount of reactant consumed. In the reaction between hydrogen and oxygen,

     1/2H_2(g) + O_2(g) ---> H₂O_(g) H = -286 kJ

     The equation says that when 1 mol of hydrogen is combined with 0.5 moles of oxygen, 1 mol of water is formed and 286 kJ of energy is liberated. If 2 moles of hydrogen are combined with 1 mol of oxygen to form 2 moles of water the amount of energy produced is twice as much, or 572 kJ.

2. The enthalpy change for a reaction is equal in magnitude and opposite in sign to H for the reverse reaction.

   • For the reaction, 1/2H_2(g) + O_2(g) ---> H₂O_(g) H = -286 kJ

     if the reaction is reversed,

     H₂O_(g) ---> 1/2H_2(g) + O_2(g) H = +286 kJ

3. The enthalpy of the reaction depends on the state of the reactants and products.

   • For the reaction, 1/2H_2(g) + O_2(g) ---> H₂O_(g) H = -286 kJ

     however, if the state of the water formed is gaseous instead of liquid H = - 242 kJ. Changing the phase of a substance involves a change in the enthalpy. In this example, an additional amount of energy is required to change water in the liquid phase to water in the vapor phase (44 kJ).

     For meaningful comparisons of heats of reaction chemists agree to specify the physical state of all substances in the reaction and the temperature at which the reaction was measured. If the reactants and products are at 25 C and 1 atmosphere they are referred to standard state enthalpies and the enthalpy of the reaction is written as H. Unless otherwise indicated all the reactions will have the reactants and products in their standard states.

4. Hess' law says, if a reaction is carried out in a series of steps, H for the reaction will equal the sum of the enthalpy changes for each step.

   • In order to demonstrate this property of enthalpy I need to define state function. Both enthalpy, H and internal energy, E are examples of state functions, in that they are properties of a system which are determined by specifying its condition or its state. The value of a state function does not depend on the history of the sample, only on its current condition. A state function does not depend on the path used to get the system to that state. Mathematically this statement can be expressed as,

     X = X_final - X_initial

     For X to be a state function X is the same independent of how the system is changed from the initial state to the final state. Let's consider an analogy to this in the form of a trip. If we travel by driving from Stillwater, Oklahoma (elevation 913 ft, latitude 97 degree 0 ', longitude 36 degree 0 ') to Bellingham, Washington (elevation 0 ft, latitude 122 degree 30 ', longitude 48 degree 50 ') there are a large number of routes that could be selected. Properties of the different routes that are not state functions are, distance, cost, tire wear and time. Properties that are state functions are the difference in altitude between Stillwater and Bellingham, the difference in longitude or latitude. These properties are all state functions. They only depend on the initial and final point of the trip, not on what happens between the initial point and the final point of the trip.

     Returning to the fourth property, enthalpy is a state function. It does not depend on how we reached a particular state of the system, only on the initial and final states.

     Hess's Law - in going from a particular set of reactants to a particular set of products, the enthalpy change is the same whether the reaction takes place in one step or in a series of steps. H for the overall reaction will be equal to the sum of the enthalpy changes of each step.

Lets consider several sample problems to demonstrate how we apply Hess' Law and several other properties of enthalpy.

Sample Problem #1 (Hess' Law);

Sample Problem #2 (Hess' Law);

Sample Problem #3 (Hess' Law);

As you might imagine it might be possible to experimentally collect H data for a number of reactions, tabulate these reactions and their corresponding enthalpy, and then use those reactions and Hess' Law to calculate the H for other reactions. But to be as efficient as possible a particular type of reaction is selected. The type of reaction is called a formation reaction. A formation reaction is defined 1 mole of a compound in its standard state is formed from its elements in their standard states. I have already shown how the magnitude of the enthalpy depends on the temperature, pressure, state of the reactants and products, so a standard state is defined as the state of a substance at 25 C and 1 atmosphere pressure. The heat associated with this reaction, at constant pressure, is the standard heat of formation, H_f. We have already encountered three examples of standard heat of formations, H_f for CO_(g), CO_2(g) and H₂O_(l).

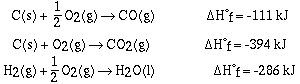
Recall that the enthalpy change for a reaction is given as;

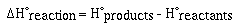
For the formation of CO₂ we would write,

We are only able to determine the change, H, in enthalpy for a chemical reaction. We do not know the enthalpy for a substance. By convention the enthalpy of an element in its standard state is zero. Therefore,

So we can prepare a list of standard heats of formation for compounds.

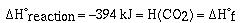
This list of heats (enthalpies) of formation can be used to calculate heats of reactions. To do this we use the equation,

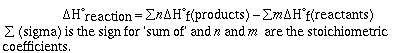
Lets do some sample problems;

Sample Problem #1 (Heat of Formation);

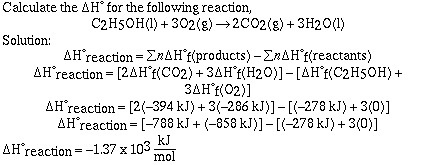
Sample Problem #2;

Sample Problem #3 (Heat of Formation);