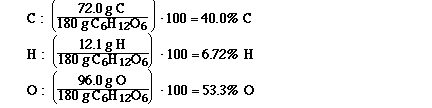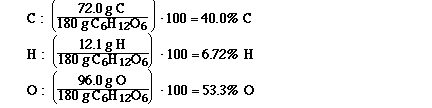Determine the formula of a compound which is
40.0% carbon, 6.72% hydrogen and 53.3% oxygen.
To solve this problem the most important thing is
to remember what a formula is...? It is the ratio of
moles of the elements in the compound! Knowing this
we can answer this question. We need to determine the
mol of each of the elements in this compound, i.e,
mol of carbon, mol of hydrogen and mol of oxygen. But
how do we do that just given the percentage
composition? We do it by assuming an amount of grams
of the compound, and since I gave you the pecent
composition of each elemetn the easiest amount to
assume is 100 g!
Because by assuming 100 g of the compound you
would have 40.0 g of carbon, 6.72 grams of hydrogen
and 53.3 grams of oxygen. And now that we have grams
of each of the elements it is easy to calculate the
number of moles of each element.

These are the mol of each element in the sample
of the compound. So now what do we do with these mol?
The next step is to take the mol and find the
simplest ratio of the mol of the elements. The
formula is the ratio of the mol of the elements and
so we need to determine the simplest ratio.
To do this we must divide each of the mol by the
smallest number of mol, that will give us our
simplest ratio.
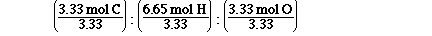
Which is, 1 mol C : 2 mol H : 1 mol O. So the
simplest ratio is CH2O. Why didn't we get
C6H12O6? Because
this type of calculation will only reveal the
simplest, or empirical formula of the compound. To
get the actual formula we must know molar mass of the
compound. In this case the molar mass is 180 grams.
The empirical mass is 30 grams. By determining the
factor which relates the empirical mass to the molar
mass we can determine the molecular formula of the
compound from the empirical formula. This is done the
following way,
empirical mass x n = molecular
mass
30 g x n = 180 g
n = 6
This tells us that the molar mass is
six times the empirical mass, for that to happen the
actual formula of the compound is 6 times the
empirical formula, (CH2O)6 or C6H12O6.
|