We need to determine the mathematical relationship between degrees C and degrees F. Here is an animation determining this relationship. This data was obtained by simultaneously measuring the temperature of a sample of ethanol in both degrees C and degrees F. This data is plotted with degrees F on the y-axis and degrees C on the x-axis. To begin the problem we must determine the range of the scale on both axis. On the y-axis the data ranges from -103 to +172, so we'll set a range of -125 to +175 in 25 degrees increments. On the x-axis the scale will range from -100 to +100 degrees C. By using these scales we'll be able to plot all of the data points.

So now plot the data. In the animation each pair of data points is identified as the data is plot on the graph. Next draw the best straight line through the data. The general equation for a straight line is given as y = mx + b where m is the slope of the line and b is the intercept on the y-axis at x = 0.

First determine the slope of the line. Select two points which fall exactly on the line. Usually these two points are not data points. The slope is determined by measuring the change in y (rise) and dividing by the change in x (run). So selecting the two data points and determine the rise, and then the run. The ratio is 100 divided by 55, which nearly 99 divided by 55, which is 9/5's.

The y- intercept can be determined by moving the y-axis over to the point where the line intersects with x=0. We see this is at 32.

So putting the results together we can determine the equation for the line.
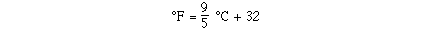